 Problem A. 573. (November 2012)
Problem A. 573. (November 2012)
A. 573. Let D={0,1,2,...,9} be the set of decimal digits, and let R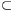 D×D be a set of ordered pairs of digits. An infinite sequence (a1,a2,a3,...) of digits is said to be compatible with R if (aj,aj+1)
D×D be a set of ordered pairs of digits. An infinite sequence (a1,a2,a3,...) of digits is said to be compatible with R if (aj,aj+1)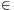 R for all positive integer j. Determine the smallest positive integer K with the property that if an arbitrary set R
R for all positive integer j. Determine the smallest positive integer K with the property that if an arbitrary set R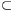 D×D is compatible with at least K distinct digit sequences then R is compatible with infinitely many digit sequences.
D×D is compatible with at least K distinct digit sequences then R is compatible with infinitely many digit sequences.
Based on the 5th problem of CIIM 2012, Guanajuato, Mexico
(5 pont)
Deadline expired on December 10, 2012.
Statistics:
15 students sent a solution. 5 points: Ágoston Péter, Fehér Zsombor, Janzer Olivér, Maga Balázs, Omer Cerrahoglu, Vályi András, Williams Kada, Zilahi Tamás. 4 points: Herczeg József, Ioan Laurentiu Ploscaru. 2 points: 2 students. 1 point: 1 student. 0 point: 2 students.
Problems in Mathematics of KöMaL, November 2012
