Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation

Already signed up?
New to KöMaL?

Problem A. 575. (December 2012)

A. 575. Prove that if $S\subset\{1,\ldots,n\}$ and $|S|>\frac{n}3$ , then it is possible to select at most four, not necessarily distinct elements from S, whose sum is a power of 2.

Proposed by: Sándor Kiss, Budapest

(5 pont)

Deadline expired on January 10, 2013.

Solution. The origin of the problem is the book Additive Number Theory: Inverse Problems and the Geometry of Sumsets by Melvyn B. Nathanson (pages 31-33.).

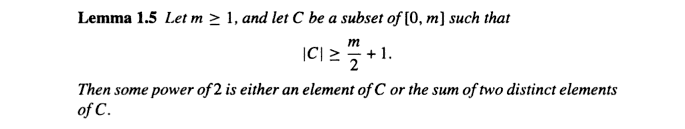
Statistics:

1 student sent a solution.

0 point: 1 student.

Problems in Mathematics of KöMaL, December 2012