Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem A. 586. (March 2013)

A. 586. Two convex quadrilaterals have side lengths a1, a2, a3, a4, and A1, A2, A3, A4; their areas are t and T, respectively. Show that

16tT \le \sum_{i=1}^4 a_i^2 \big(A_{i+1}^2+A_{i+2}^2+A_{i+3}^2-A_i^2\big) + 4a_1A_2a_3A_4 + 4A_1a_2A_3a_4.

(The indices are used modulo 4.)

(5 pont)

Deadline expired on April 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat.

Lemma.

16t^2 \le \prod_{i=1}^4 (a_{i+1}+a_{i+2}+a_{i+3}-a_i),

és egyenlőség akkor áll, ha a négyszög húrnégyszög.

Bizonyítás. A területet úgy írjuk fel, hogy a négyszöget két háromszögre bontjuk. Jelölje \varphi az a1 és a2, 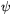\psi pedig az a3 és a4 oldalak közötti szöget; ekkor tehát

t = \frac12 a_1a_2\sin\varphi + \frac12 a_3a_4\sin\psi.

A két háromszögre felírva a koszinusztételt

a12+a22-2a1a2cos \varphi=a32+a42-2a3a4cos \psi;

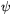átrendezve

a12+a22-a32-a42=2(a1a2cos \varphi-a3a4cos \psi).

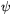Ezután

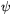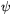16t2+(a12+a22-a32-a42)2=4(a1a2sin \varphi+a3a4sin \psi)2+4(a1a2cos \varphi-a3a4cos \psi)2=            

            =4a12a22+4a32a42-8a1a2a3a4cos (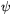\varphi+\psi)\le4a12a22+4a32a42+8a1a2a3a4=4(a1a2+a3a4)2.

Akkor van egyenlőtlenség, ha cos (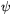\varphi+\psi)=-1, azaz 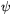\varphi+\psi=180o.

A becslést átrendezve,

16t2\le4(a1a2+a3a4)2-(a12+a22-a32-a42)2=(2(a1a2+a3a4)+(a12+a22-a32-a42))(2(a1a2+a3a4)-(a12+a22-a32-a42))=(*)

=((a1+a2)2-(a3-a4)2))((a3+a4)2-(a1-a2)2))=(a1+a2+a3-a4)(a1+a2-a3+a4)(a3+a4+a1-a2)(a3+a4-a1+a2).

(Bővebben lásd itt.)

A feladat megoldásához írjuk fel a Lemmát mindkét négyszögre a következő alakban (ez valójában a (*) sor, csak az a2 és az a3 változok szerepét felcseréltük):

16t2+(a12+a32-a22-a42)2\le4(a1a3+a2a4)2

16T2+(A12+A32-A22-A42)2\le4(A1A3+A2A4)2

A Cauchy-Schwarz-Bunyakovszkij egyenlőtlenségből

16tT+(a12+a32-a22-a42)(A12+A32-A22-A42)\le

\le \sqrt{16t^2 + (a_1^2+a_3^2-a_2^2-a_4^2)^2} \sqrt{16T^2 + (A_1^2+A_3^2-A_2^2-A_4^2)^2} \le 4(a_1a_3+a_2a_4)(A_1A_3+A_2A_4) =

=4a1A2a3A4+4A1a2A3a4+4a1a3A1A3+4a2a4A2A4\le4a1A2a3A4+4A1a2A3a4+2(a12A32+a32A12)+2(a22A42+a42A22).

Ezért

16tT\le4a1A2a3A4+4A1a2A3a4+2(a12A32+a32A12+a22A42+a42A22)-(a12+a32-a22-a42)(A12+A32-A22-A42)=

= \sum_{i=1}^4 a_i^2 \big(A_{i+1}^2+A_{i+2}^2+A_{i+3}^2-A_i^2\big) + 4a_1A_2a_3A_4 + 4A_1a_2A_3a_4.

A becslésekből leolvasható, hogy egyenlőség akkor van, ha két hasonló húrnégyszögről van szó.

Statistics:

3 students sent a solution.
5 points:Janzer Olivér, Szabó 789 Barnabás.
1 point:1 student.

Problems in Mathematics of KöMaL, March 2013