 Problem A. 591. (May 2013)
Problem A. 591. (May 2013)
A. 591. There is given a convex quadrilateral ABCD and some points P, Q, R and S on the line segments AB, BC, CD and DA, respectively. The line segments PR and QS meet at T. Suppose that each of the the quadrilaterals APTS, BQTP, CRTQ and DSTR have an inscribed circle. Prove that the quadrilateral ABCD also has an inscribed circle.
(5 pont)
Deadline expired on June 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Használjuk az ábra betűzését.
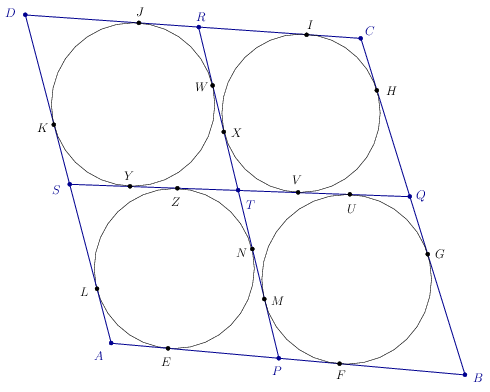
Mivel
EF+IJ=ZU+VY=ZT+TU+VT+TY=NT+TM+XT+TW=NW+XM=LK+HG,
ezért
AB+CD=(AE+EF+FB)+(CI+IJ+JD)=(AL+LK+KD)+(CH+HG+GB)=AD+BC.
Az ABCD négyszög szemközti oldalainak összege mindkét pár esetén ugyanaz, tehát ABCD érintőnégyszög.
Statistics:
14 students sent a solution. 5 points: Ágoston Péter, Bereczki Zoltán, Bodnár Levente, Cyril Letrouit, Fehér Zsombor, Gyulai-Nagy Szuzina, Janzer Olivér, Kovács 162 Viktória, Kúsz Ágnes, Machó Bónis, Sárosdi Zsombor, Szabó 789 Barnabás, Williams Kada. 4 points: Herczeg József.
Problems in Mathematics of KöMaL, May 2013
