 Problem A. 593. (September 2013)
Problem A. 593. (September 2013)
A. 593. Let a, b, c be positive real numbers. Prove that
Based on problem 1 of MEMO 2013
(5 pont)
Deadline expired on October 10, 2013.
Solution. The function is concave on (0,
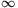 ), therefore
), therefore
holds for all u,x>0. In particular, for u=8a3 and x=7a2b+1 we get
Summing up the analogous upper bouds on the other two terms,
Statistics:
39 students sent a solution. 5 points: Ágoston Péter, Balogh Tamás, Barna István, Bereczki Zoltán, Di Giovanni Márk, Fehér Zsombor, Forrás Bence, Ioan Laurentiu Ploscaru, Janzer Barnabás, Maga Balázs, Makk László, Nagy-György Pál, Schwarcz Tamás, Simon 047 Péter, Szabó 789 Barnabás, Szőke Tamás, Tossenberger Tamás, Williams Kada. 4 points: Emri Tamás, Gyulai-Nagy Szuzina, Herczeg József, Kúsz Ágnes, Machó Bónis, Paulovics Zoltán, Petrényi Márk. 3 points: 10 students. 2 points: 2 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, September 2013
