 Problem A. 594. (September 2013)
Problem A. 594. (September 2013)
A. 594. The convex quadrilateral ABCD has an inscribed circle which is tangent to the sides AB and BC at E and F, respectively. The diagonal AC meets the inscribed circle at P and Q; the point Q is located between A and P. Show that the lines BD, EP and FQ are concurrent.
(5 pont)
Deadline expired on October 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás (vázlat) A feladatot projektív geometriai eszközökkel oldjuk meg; felhasználjuk a körre vonatkozó polaritás néhány jól ismert tulajdonságát. (Ld. pl. itt, itt vagy itt.)
Legyen G és H a beírt kör érintési pontja a CD, illetve a DA oldalon. Messe a beírt kör a BD átlót az R és az S pontban (BR<BS), továbbá legyen O az EG és az FH szakasz metszéspontja. Jól ismert, hogy az AC, BD, EG és FH egyenesek egy ponton mennek át, tehát AC és BD is átmegy O-n.
Legyen X és Y a BD, illetve az AC egyenesnek a beírt körre vonatkozó pólusa. Szintén ismert, hogy az AC és BD egyensek konjugáltak, azaz átmennek egymás pólusán: X az AC, Y pedig a BD egyenesen van.
Mivel Y polárisa az AQPC egyenes, az YP és YQ szakaszok az Y pontból a beírt körhöz húzott érintők; hasonlóképpen, XR és XS az X pontból húzott érintők. Az A és Y pontok konjugáltak, mert A rajta van az Y pont AC polárisán, ezért Y is rajta van A polárisán, ami az EH egyenes. Tehát E,H,Y egy egyenesen van. Hasonlóan láthatjuk, hogy az F,G,Y, az E,F,X, iletve a G,H,X pontok egy egyenesen vannak.
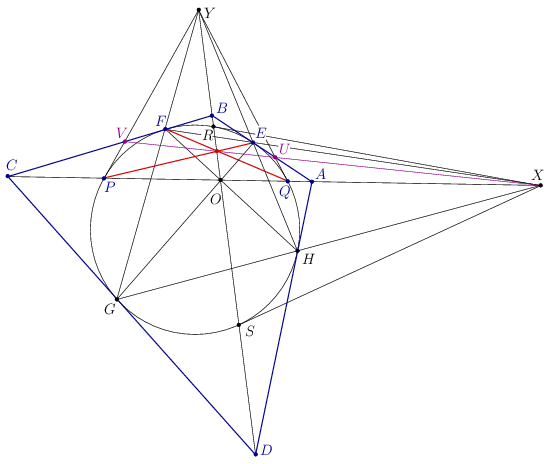
Legyen U az AB és YQ, V pedig a BC és YP egyenesek metszéspontja. A BUYV érintőnégyszögben is igaz, hogy a BY és UV átlók, továbbá a szemközti érintési pontokat összekötő EP és FQ egyenesek egy ponton mennek át. (Az is igaz, hogy az UV egyenes átmegy X-en.)
2. megoldás (vázlat) Legyen ismét G és H a beírt kör érintési pontja a CD, illetve a DA oldalon, és legyen O az EG és az FH szakasz metszéspontja. Az O pont a kör belsejében van.
Ismert, hogy az ábrát lehetséges középpontosan egy másik síkra vetíteni úgy, hogy a beírt kör képe kör legyen, az O pont O' képe pedig a vetített kör középpontja. (A részletes bizonyítást ld. pl. Reiman István: Geometria és határterületei [1999], 384-387. old.).
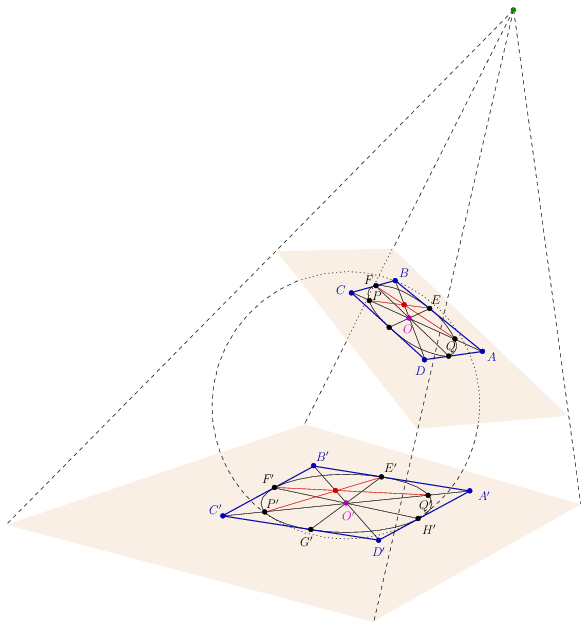
Az X pont képét X'-szel jelölve, az A'B'C'D' négyszögben E'G' és F'H' a beírt kör átmérői, következésképp A'B'C'D' egy rombusz. Az E'P' és F'H' szakaszok szimmetrikusak a rombusz B'D' átlójára, ezért metszéspontjuk az átlón van.
Az eredeti síkra visszavetítve kapjuk, hogy EP, FQ és BD egy ponton megy át.
Statistics:
15 students sent a solution. 5 points: Fehér Zsombor, Herczeg József, Homonnay Bálint, Ioan Laurentiu Ploscaru, Janzer Barnabás, Kabos Eszter, Machó Bónis, Maga Balázs, Petrényi Márk, Simon 047 Péter, Szabó 789 Barnabás, Szőke Tamás, Williams Kada. 1 point: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, September 2013
