 Problem A. 682. (November 2016)
Problem A. 682. (November 2016)
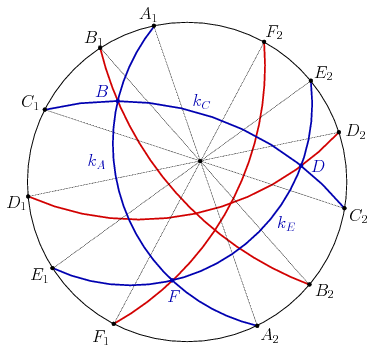
A. 682. Let \(\displaystyle A_1B_1C_1D_1E_1F_1A_2B_2C_2D_2E_2F_2\) be a cyclic dodecagon such that its diagonals \(\displaystyle A_1A_2\), \(\displaystyle B_1B_2\) and \(\displaystyle C_1C_2\) are concurrent, the diagonals \(\displaystyle A_1A_2\), \(\displaystyle E_1E_2\) and \(\displaystyle F_1F_2\) are concurrent, the diagonals \(\displaystyle C_1C_2\), \(\displaystyle D_1D_2\) and \(\displaystyle E_1E_2\) are concurrent, and finally the diagonals \(\displaystyle B_1B_2\), \(\displaystyle D_1D_2\) and \(\displaystyle F_1F_2\) are concurrent.Let \(\displaystyle k_A\), \(\displaystyle k_C\) and \(\displaystyle k_E\) be three circular arcs in the interior of the dodecagon's circumcircle such that \(\displaystyle k_A\) connects \(\displaystyle A_1\) and \(\displaystyle A_2\), \(\displaystyle k_C\) connects \(\displaystyle C_1\) and \(\displaystyle C_2\), and \(\displaystyle k_E\) connects \(\displaystyle E_1\) and \(\displaystyle E_2\). Let the intersection points of the three arcs be \(\displaystyle B=k_A\cap k_C\), \(\displaystyle D=k_C\cap k_E\) and \(\displaystyle F=k_A\cap k_E\). Prove that the circular arcs \(\displaystyle B_1BB_2\), \(\displaystyle D_1DD_2\) and \(\displaystyle F_1FF_2\) are concurrent. (These arcs degenerate to line segments if their specified points are collinear.)
Marcello Mamino, Dresden, Luca Ghidelli, Ottawa and Ilya Bogdanov, Moscow
(5 pont)
Deadline expired on December 12, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen \(\displaystyle A_1A_2\), \(\displaystyle B_1B_2\) és \(\displaystyle C_1C_2\) közös pontja a \(\displaystyle P\) pont, \(\displaystyle C_1C_2\), \(\displaystyle D_1D_2\) és \(\displaystyle E_1E_2\) közös pontja a \(\displaystyle Q\) pont, \(\displaystyle A_1A_2\), \(\displaystyle E_1E_2\) és \(\displaystyle F_1F_2\) közös pontja az \(\displaystyle R\) pont, \(\displaystyle B_1B_2\), \(\displaystyle D_1D_2\) és \(\displaystyle F_1F_2\) közös pontja az \(\displaystyle S\) pont.
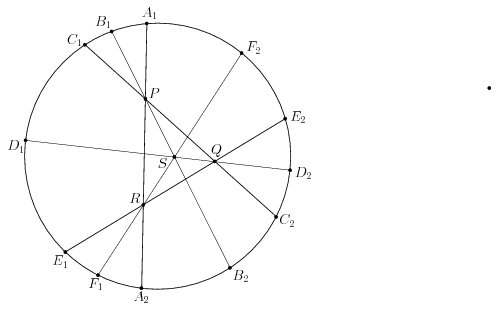
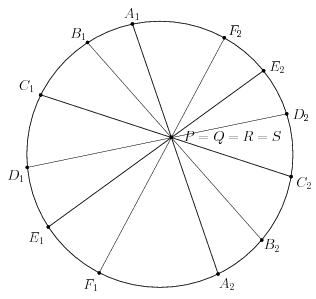
Ha az \(\displaystyle A_1A_2\), \(\displaystyle C_1C_2\), \(\displaystyle E_1E_2\) szakaszok nem mennek át egy ponton, akkor a \(\displaystyle P,Q,R\) pontok egy háromszöget alkotnak. A \(\displaystyle B_1B_2\), \(\displaystyle D_1D_2\), \(\displaystyle F_1F_2\) egyenesek a \(\displaystyle RP\), \(\displaystyle PQ\), illetve \(\displaystyle QR\) szakaszt egy-egy belső pontjukban metszik, és \(\displaystyle S\) belső pontja a \(\displaystyle QRP\) háromszögnek (baloldali ábra). Nevezzük ezt "általános" esetnek. Ezzel szemben, ha az \(\displaystyle A_1A_2\), \(\displaystyle C_1C_2\), \(\displaystyle E_1E_2\) szakaszok egy ponton mennek át, akkor \(\displaystyle P=Q=R\), és ezen a ponton a \(\displaystyle B_1B_2\), \(\displaystyle D_1D_2\), \(\displaystyle F_1F_2\) szakaszok is átmennek. Ilyenkor tehát az \(\displaystyle A_1A_2\), \(\displaystyle B_1B_2\), \(\displaystyle C_1C_2\), \(\displaystyle D_1D_2\), \(\displaystyle E_1E_2\), \(\displaystyle F_1F_2\) szakaszok mind egy ponton mennek át (jobboldali ábra) Nevezzük ezt "elfajuló" esetnek.
Mint több versenyzők is észrevette, az elfajuló esetben az állítás hamis:
A továbbiakban ezért csak az általános esetet vizsgáljuk, amikor az \(\displaystyle A_1A_2\), \(\displaystyle C_1C_2\) és \(\displaystyle E_1E_2\) egyenesek egyike sem megy át az \(\displaystyle S\) ponton.
Helyezzük el az ábrát a derékszögű koordináta-rendszerben úgy, hogy a tizenkétszög köré írt kör legyen az egységkör. Azt fogjuk mondani, hogy egy \(\displaystyle \mathcal{H}\) ponthalmaznak egy \(\displaystyle f\) függvény "egyenlete", ha a sík bármely \(\displaystyle X=(x,y)\) pontjára \(\displaystyle f(X)=0\) akkor és csak akkor teljesül, ha \(\displaystyle X\in\mathcal{H}\). Az alakzatokra és az egyenletükre ugyanazt a jelölést fogjuk használni, így pl. \(\displaystyle k_A\) jelenti \(\displaystyle A_1AA_2\) kört (vagy egyenest) és annak egy egyenletét is; ez nem fog zavart okozni.
Jól tudjuk, hogy minden egyenesnek van lineáris egyenlete, és minden körnek van olyan másodfokú egyenlete, amelynek másodfokú része \(\displaystyle c|OX|^2=c(x^2+y^2)\) alakú. A körülírt kör egy egyenlete \(\displaystyle \varOmega(X)=|OX|^2-1\).
Legyen az \(\displaystyle A_1A_2\), \(\displaystyle C_1C_2\), \(\displaystyle E_1E_2\) egyenesek egy-egy lineáris egyenlete \(\displaystyle \ell_A\), \(\displaystyle \ell_C\), illetve \(\displaystyle \ell_E\). Mivel a három egyenes nem megy át az \(\displaystyle S\) ponton, \(\displaystyle \ell_A(S)\ne0\), \(\displaystyle \ell_C(S)\ne0\), és \(\displaystyle \ell_E(S)\ne0\); az egyenleteket alkalmas konstansokkal megszorozva elérhetjük, hogy egyúttal \(\displaystyle \ell_A(S)=\ell_C(S)=\ell_E(S)=1\) is teljesüljön.
Az \(\displaystyle \ell_B=\ell_A-\ell_C\) egyenlet teljesül a \(\displaystyle P\) és az \(\displaystyle S\) pontra is, mert \(\displaystyle P\) közös pontja az \(\displaystyle \ell_A\) és \(\displaystyle \ell_C\) egyeneseknek, így \(\displaystyle \ell_A(P)=\ell_C(P)=0\), továbbá az egyenletek választása szerint \(\displaystyle \ell_A(S)=\ell_C(S)=1\). Ezért \(\displaystyle \ell_B\) a \(\displaystyle B_1PSB_2\) egyenes egy egyenlete. A betűzés ciklikus cseréjével, hasonlóan látjuk, hogy a \(\displaystyle D_1QSD_2\) egyenes egy egyenlete \(\displaystyle \ell_D=\ell_C-\ell_E\), illetve az \(\displaystyle F_1RSF_2\) egyenes egy egyenlete \(\displaystyle \ell_F=\ell_E-\ell_A\).
Most írjuk fel a \(\displaystyle k_A\), \(\displaystyle k_C\) és \(\displaystyle k_E\) körök egyenleteit. Tetszőleges \(\displaystyle c_1\) valós számra az \(\displaystyle \ell_A+c_1\cdot\varOmega\) egyenletű alakzat — ami vagy kör, vagy egyenes — átmegy az \(\displaystyle A_1\) és \(\displaystyle A_2\) pontokon, mivel \(\displaystyle \ell_A\) és \(\displaystyle \varOmega\) értéke ezekben a pontokban \(\displaystyle 0\). A \(\displaystyle c_1\) számot megválaszthatjuk úgy, hogy az egyenlet a \(\displaystyle k_A\) kör egy további pontjában is teljesüljön. A \(\displaystyle k_A\) körnek tehát van egy \(\displaystyle k_A=\ell_A+c_1\cdot\varOmega\) alakú egyenlete valamilyen alkalmas \(\displaystyle c_1\) konstanssal. Hasonlóan, a \(\displaystyle k_C\) és \(\displaystyle k_E\) körök egyenletét is felírhatjuk \(\displaystyle k_C=\ell_C+c_2\cdot\varOmega\), illetve \(\displaystyle k_E=\ell_E+c_3\cdot\varOmega\) alakban, alkalmas \(\displaystyle c_2\) és \(\displaystyle c_3\) konstansokkal.
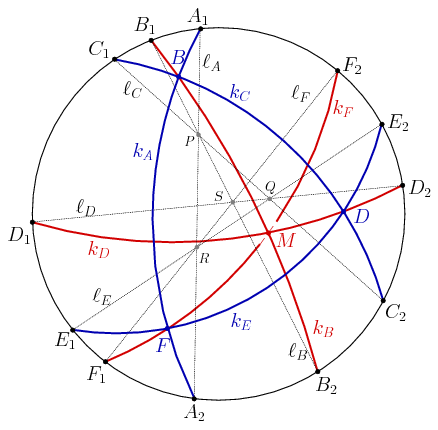
Most vizsgáljuk a \(\displaystyle B_1BB_2\) kört. Azt állítjuk, hogy ennek egyenlete \(\displaystyle k_A-k_C\). Nyilván elég ellenőrizni, hogy ez az egyenlet teljesül a \(\displaystyle B_1\), \(\displaystyle B_2\) és \(\displaystyle B\) pontokra. A \(\displaystyle B\) pont a \(\displaystyle k_A\) és \(\displaystyle k_C\) körök metszéspontja, így \(\displaystyle k_A(B)=k_C(B)=0\). A \(\displaystyle B_1\) pont a körülírt körön van, ezért \(\displaystyle k_A(B_1)=\ell_A(B_1)+c_1\varOmega(B_1)=\ell_A(B_1)\) és ugyanígy \(\displaystyle k_C(B_1)=\ell_C(B_1)+c_2\varOmega(B_1)=\ell_C(B_1)\), tehát \(\displaystyle k_A(B_1)-k_C(B_1)=\ell_A(B_1)-\ell_C(B_1) = \ell_B(B_1)=0\). Hasonlóan teljesül, hogy \(\displaystyle k_B(B_2)=k_A(B_2)-k_C(B_2)=0\). Ezzel igazoltuk, hogy a \(\displaystyle B_1BB_2\) kör egyenlete \(\displaystyle k_B=k_A-k_C\). A betűzés ciklikus cseréjével, ugyanígy kaphatjuk, hogy a \(\displaystyle D_1DD_2\) kör egyenlete \(\displaystyle k_D=k_C-k_E\), az \(\displaystyle F_1FF_2\) kör egyenlete \(\displaystyle k_F=k_E-k_A\).
Vegyük észre, hogy a három kör egyenletének összege \(\displaystyle 0\):
\(\displaystyle k_B + k_D + k_F = (k_A-k_C) + (k_C-k_E) + (k_E-k_A) \equiv 0. \tag{1} \)
Ha \(\displaystyle k_B\) és \(\displaystyle k_D\) körívek metszéspontja \(\displaystyle M\), akkor \(\displaystyle k_B(M)=k_D(M)=0\); az (1) azonosság alapján \(\displaystyle k_F(M)=0\), vagyis a \(\displaystyle k_F\) kör is átmegy az \(\displaystyle M\) ponton. Ezzel az állítást igazoltuk az általános esetben.
Statistics:
9 students sent a solution. 5 points: Matolcsi Dávid, Németh 123 Balázs, Williams Kada. 4 points: Bukva Balázs, Egri Máté, Imolay András, Kerekes Anna. 1 point: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, November 2016
