 Problem A. 685. (December 2016)
Problem A. 685. (December 2016)
A. 685. Let \(\displaystyle AB\) and \(\displaystyle CD\) be two chords in a circle \(\displaystyle \Omega\). Choose a circle \(\displaystyle \omega\) tangent to the segments \(\displaystyle AB\) and \(\displaystyle CD\) at their interior points \(\displaystyle M\) and \(\displaystyle N\) respectively, and let \(\displaystyle \omega\) intersect \(\displaystyle \Omega\) at \(\displaystyle P\) and \(\displaystyle Q\). Suppose that a third circle \(\displaystyle \omega'\), distinct from \(\displaystyle \Omega\) and \(\displaystyle \omega\), and also passing through \(\displaystyle P\) and \(\displaystyle Q\), meets the line \(\displaystyle MN\) at \(\displaystyle M'\) and \(\displaystyle N'\). Prove that the points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle M'\), and \(\displaystyle N'\) lie on a conic section that is tangent to \(\displaystyle \omega'\) at \(\displaystyle M'\) and \(\displaystyle N'\).
(Proposed by: Ilya Bogdanov and Pavel Kozhevnikov, Moscow)
(5 pont)
Deadline expired on January 10, 2017.
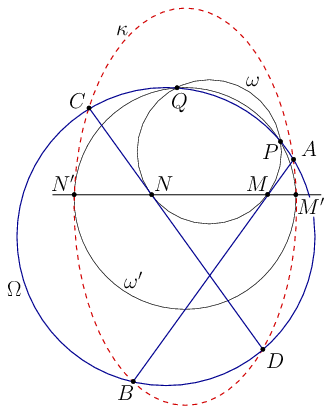
Solution. Let \(\displaystyle f(x)=0\), \(\displaystyle g(x)=0\), and \(\displaystyle m(x)=0\) be equations (with degrees \(\displaystyle 2\), \(\displaystyle 2\), and \(\displaystyle 1\), respectively) of the circles \(\displaystyle \Omega\), \(\displaystyle \omega\), and the line \(\displaystyle MN\), respectively.
The pencil of conics generated by \(\displaystyle g(x)=0\) and \(\displaystyle m(x)^2=0\) consists of all conics which have double intersections with \(\displaystyle \omega\) at \(\displaystyle M\) and \(\displaystyle N\); thus the union of the lines \(\displaystyle AB\) and \(\displaystyle CD\) lies in this pencil, so its equation is
| \(\displaystyle g(x)+\alpha m(x)^2=0 \qquad \text{with some nonzero \(\displaystyle \alpha\in\mathbb{R}\)}. \) | \(\displaystyle {(AB\cup CD)} \) |
The pencil of circles generated by \(\displaystyle \Omega\) and \(\displaystyle \omega\) consists of all circles passing through \(\displaystyle P\) and \(\displaystyle Q\) (including the line \(\displaystyle PQ\) as a degenerate case). Thus the circle \(\displaystyle \omega'\) lies in this pencil, so its equation is
| \(\displaystyle g(x)+\beta f(x)=0 \qquad \text{with some nonzero \(\displaystyle \beta\in\mathbb R\)}. \) | \(\displaystyle {(\omega')} \) |
Now consider the conic \(\displaystyle \kappa\) with the equation
| \(\displaystyle g(x)+\alpha m(x)^2+\beta f(x)=0. \) | \(\displaystyle {(\kappa)} \) |
This conic lies in the pencil of conics generated by \(\displaystyle AB\cup CD\) and \(\displaystyle \Omega\), so \(\displaystyle \kappa\) passes though their common points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), and \(\displaystyle D\). On the other hand, this equation is a linear combination of \(\displaystyle m(x)^2=0\) and the equation of \(\displaystyle \omega'\); thus \(\displaystyle \kappa\) has double intersections with \(\displaystyle \omega'\) at \(\displaystyle M'\) and \(\displaystyle N'\), which means that \(\displaystyle \kappa\) is tangent to \(\displaystyle \omega'\) at \(\displaystyle M'\) and \(\displaystyle N'\). Hence \(\displaystyle \kappa\) is the required conic.
For completeness, notice that the equation \(\displaystyle \kappa\) cannot be trivial because the points \(\displaystyle P\) and \(\displaystyle Q\) do not satisfy it.
Remark. As a corollary, one may obtain the following (known) fact: There exists a circle through \(\displaystyle P\) and \(\displaystyle Q\) tangent to \(\displaystyle AD\) and \(\displaystyle BC\), and the points of tangency lie on the line \(\displaystyle MN\).
Statistics:
3 students sent a solution. 5 points: Bukva Balázs, Matolcsi Dávid, Williams Kada.
Problems in Mathematics of KöMaL, December 2016
