 Problem B. 3805. (March 2005)
Problem B. 3805. (March 2005)
B. 3805. The lengths of the sides of a cyclic quadrilateral are a, b, c, d, respectively, its perimeter is 2s and the measure of the angle of the sides a and b is  . Prove that
. Prove that
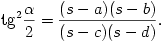
(4 pont)
Deadline expired on April 15, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Először alakítsuk át a jobboldali kifejezést:
Legyen e annak az átlónak a hossza, amely az a és d hosszúságú oldalak metszéspontjából indul. Mivel a c és d oldalak által bezárt szög 180o- , ennek a szögnek a koszinusza -cos
, ennek a szögnek a koszinusza -cos  lesz. A koszinusz tétel alapján tehát
lesz. A koszinusz tétel alapján tehát
a2+b2-2abcos  =e2=c2+d2+2cdcos
=e2=c2+d2+2cdcos  .
.
Ennek alapján
Statistics:
87 students sent a solution. 4 points: 80 students. 3 points: 3 students. 0 point: 2 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, March 2005
