 Problem B. 3812. (April 2005)
Problem B. 3812. (April 2005)
B. 3812. Find all positive integers n, such that
a) 7399|n! , but 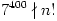 , and
, and
b) 7400|n! , but 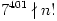 .
.
(4 pont)
Deadline expired on May 17, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az n! szám prímtényezős felbontásában a 7 kitevője
Világos, hogy ha n értékét növeljük, akkor  értéke nem csökken. Nézzük meg tehát, mennyi
értéke nem csökken. Nézzük meg tehát, mennyi  értéke, ha n=6.400=2400=74-1:
értéke, ha n=6.400=2400=74-1:
 =(73-1)+(72-1)+(7-1)=396.
=(73-1)+(72-1)+(7-1)=396.
Ha azonban n=2401=74, akkor
 =73+72+7+1=400.
=73+72+7+1=400.
Ezek szerint, ha n! osztható 7399-nel, akkor már 7400-nal is osztható lesz. Nincsen tehát olyan n érték, amelyre az a) feltétel teljesülne. A b) feltétel teljesül, ha n=2401+r, ahol 0 r
r 6 egész szám, hiszen ekkor [n/7i]=[2401/7i] teljesül minden i pozitív egész számra. Ha azonban n=2408, akkor
6 egész szám, hiszen ekkor [n/7i]=[2401/7i] teljesül minden i pozitív egész számra. Ha azonban n=2408, akkor  értékére már 401-et kapunk. A b) feltételt kielégítő n számok tehát 2401, 2402, 2403, 2404, 2405, 2406 és 2407.
értékére már 401-et kapunk. A b) feltételt kielégítő n számok tehát 2401, 2402, 2403, 2404, 2405, 2406 és 2407.
Statistics:
147 students sent a solution. 4 points: Almási 270 Gábor, Berinkei Péter, Bitai Tamás, Cseh Ágnes, Csóka Győző, Dombi Péter, Doszkocs Tamás, Dömötör Erika, Eisenberger András, Estélyi István, Gombkötő Tamás, Gyenizse Gergő, Györgyi Péter, Hartmann Zoltán, Horváth 017 Zoltán, Horváth 151 Gábor, Hujter Bálint, Károlyi Gergely, Károlyi Márton, Ketskeméty Kristóf, Kiss 243 Réka, Knipl Diána, Kómár Péter, Kónya 495 Gábor, Kovács 129 Péter, Kunovszki Péter, Kutas Péter, Mészáros Gábor, Nándori Balázs, Németh 007 Zsolt, Pap Máté, Pásztor 001 Attila, Peregi Tamás, Pesti Veronika, Petrás András, Poronyi Balázs, Sümegi Károly, Szalkai Balázs, Szalóki Dávid, Szilágyi 987 Csaba, Szilágyi Dániel, Szirmai Péter, Tóth 666 László Márton, Tóth 796 Balázs, Udvari Balázs, Ureczky Bálint, Vad Szilvia, Varga 868 András. 3 points: 66 students. 2 points: 14 students. 1 point: 9 students. 0 point: 10 students.
Problems in Mathematics of KöMaL, April 2005
