 Problem B. 3815. (April 2005)
Problem B. 3815. (April 2005)
B. 3815. A plane intersects each line segment of a closed polygon P1P2...PnP1 of the space. The intersection with the line segment PiPi+1 is the interior point Qi. Prove that
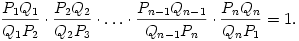
(3 pont)
Deadline expired on May 17, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A Pi pontnak a síkra vonatkozó vetülete legyen Ri. A Pn+1=P1 jelöléssel élve látható, hogy esetén PiQi:Pi+1Qi=PiRi:Pi+1Ri+1, amint az leolvasható az esetleg elfajuló PiQiRi és Pi+1QiRi+1 háromszögek hasonlóságából. Ezért a szóban forgó szorzat értéke
Statistics:
58 students sent a solution. 3 points: Antal Bálint, Balambér Dávid, Berinkei Péter, Bitai Tamás, Bock Lilla, Csaba Ákos, Cserép Gergely, Eisenberger András, Estélyi István, Fegyveres György, Fegyverneki Tamás, Fischer Richárd, Gehér György, Grósz Dániel, Győrffy Lajos, Györgyi Péter, Halász Veronika, Hartmann Zoltán, Kara Márton, Kiss 111 Viktor, Kiss 243 Réka, Knipl Diána, Kokavecz János, Kómár Péter, Kovács 129 Péter, Kovács 456 Balázs, Laczák Lili, Lamm Éva, Lorántfy Bettina, Lovász László Miklós, Lukucz Balázs, Mátyás Péter, Müller Márk, Nagy 235 János, Nagy-Baló András, Novák 125 Zsófia, Pap Máté, Pesti Veronika, Sommer Dániel, Sóvágó Sándor, Sümegi Károly, Szabó 108 Tamás, Szalkai Balázs, Szalóki Dávid, Szentandrási István, Szirmai Péter, Szudi László, Tóth 796 Balázs, Tóthmérész Lilla, Varga 111 Péter. 2 points: 4 students. 1 point: 1 student. 0 point: 3 students.
Problems in Mathematics of KöMaL, April 2005
