Problem B. 3821. (April 2005)

B. 3821. a, b, c are positive numbers, such that a²+b²+c²=1. Find the smallest possible value of the sum

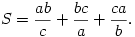
$S=\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}.$

(5 pont)

Deadline expired on May 17, 2005.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Állítjuk, hogy S² $\ge$ 3(a²+b²+c²), vagyis hogy

$\Bigl({a^2b^2+b^2c^2+c^2a^2\over abc}\Bigr)^2\ge 3(a^2+b^2+c^2).$

Ezzel ekvivalens, hogy

(a²b²+b²c²+c²a²)² $\ge$ 3a²b²c²(a²+b²+c²),

ami átrendezés után az

a⁴b⁴+b⁴c⁴+c⁴a⁴ $\ge$ a⁴b²c²+b⁴c²a²+c⁴a²b²

alakot ölti. További átrendezés során látható, hogy az

${a^4(b^2-c^2)^2+b^4(c^2-a^2)^2+c^4(a^2-b^2)^2\over 2}\ge 0$

egyenlőtlenséget kell igazolnunk, ami nyilvánvaló.

Vagyis S² $\ge$ 3, ahol egyenlőség csakis az a²=b²=c² esetben állhat fönn. Az S összeg legkisebb lehetséges értéke tehát $\sqrt{3}$ , mely értéket $a=b=c=1/\sqrt{3}$ esetén veszi fel.

Statistics:

79 students sent a solution.

5 points: 52 students.

4 points: 1 student.

3 points: 1 student.

2 points: 2 students.

1 point: 1 student.

0 point: 22 students.

Problems in Mathematics of KöMaL, April 2005

79 students sent a solution.
5 points:	52 students.
4 points:	1 student.
3 points:	1 student.
2 points:	2 students.
1 point:	1 student.
0 point:	22 students.

Already signed up?
New to KöMaL?