 Problem B. 3832. (September 2005)
Problem B. 3832. (September 2005)
B. 3832. P is an arbitrary point of the hypotenuse AB of a right-angled triangle ABC. The foot of the altitude drawn from vertex C is C1. The projection of P onto the leg AC is A1, and its projection onto the leg BC is B1.
a) Prove that the points P, A1, C, B1, C1 lie on a circle.
b) Prove that the triangles A1B1C1 and ABC are similar.
(3 pont)
Deadline expired on October 17, 2005.
Solution. (a) The angles  PA1C,
PA1C,  PB1C,
PB1C,  PC1C are all right angles, so points A1, B1, C1 lie on the circle of diameter PC. Due to the right angle at C, another diameter of this circle is A1B1.
PC1C are all right angles, so points A1, B1, C1 lie on the circle of diameter PC. Due to the right angle at C, another diameter of this circle is A1B1.
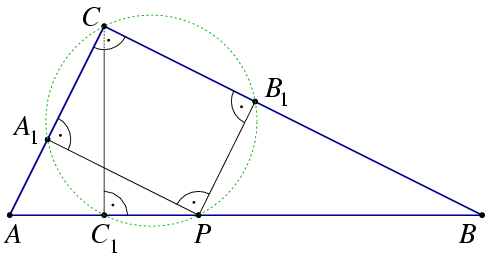
(b) From the triangles ABC and CBC1,  BAC
BAC =90o-angleABC=
=90o-angleABC= BCC1. Since quadrilateral CA1C1B1 is cyclic, B1CC1
BCC1. Since quadrilateral CA1C1B1 is cyclic, B1CC1 =B1A1C1
=B1A1C1 . Therefore, the red angles in the Figure are equal.
. Therefore, the red angles in the Figure are equal.
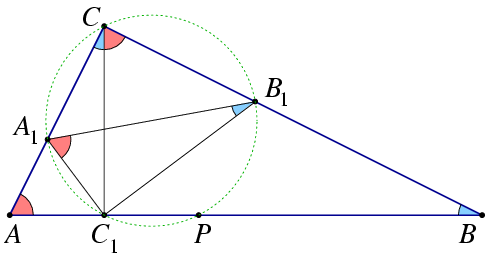
Similarly, also the blue angles are equal.
Triangles ABC and A1B1C1 are similar because they have equal angles, respectively.
Statistics:
384 students sent a solution. 3 points: 205 students. 2 points: 64 students. 1 point: 98 students. 0 point: 14 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, September 2005
