 Problem B. 3837. (September 2005)
Problem B. 3837. (September 2005)
B. 3837. Let P and Q, respectively, denote the centres of the squares ABDE and BCGH drawn on the sides AB and BC of the triangle ABC outwards. The midpoints of the sides AC and DH are R and S, respectively. Show that the points P, Q, R and S are the vertices of a square. (4 points)
(4 pont)
Deadline expired on October 17, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás.
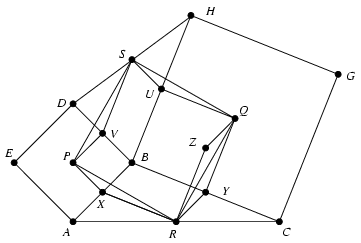
Legyenek X,Y,U és V rendre az AB,BC,BH és BD szakaszok felezőpontjai, Z pedig az Y pontnak a QR szakasz felezőpontjára vonatkozó tükörképe. Mivel az SU szakasz a BDH háromszög középvonala, SU párhuzamos és egyenlő hosszú a VB szakasszal, és így a PX szakasszal is. Hasonlóképpen az UQ és XR szakaszok is párhuzamosak és egyenlő hosszúak. Ezért az UQS - esetleg elfajuló - háromszög eltolással származtatható az XRP háromszögből, amiért is a PRQS négyszög paralelogramma. QZ párhuzamos és egyenlő hosszú az YR szakasszal, ezért BX-szel is, vagyis a PX szakaszból 90o-os elforgatással keletkezik. ZR pedig párhuzamos és egyenlő hosszú a QY szakasszal, amely viszont az XR-rel párhuzamos és egyenlő hosszú BY szakaszból keletkezik ugyancsak 90o-os elforgatással. Következésképpen a QZR háromszög a PXR háromszögből kapható meg 90o-os elforgatással, vagyis a QR szakasz merőleges a PR szakaszra, és hosszuk megegyezik. Ebből már következik, hogy a PRQS paralelogramma négyzet.
Statistics:
216 students sent a solution. 4 points: 159 students. 3 points: 24 students. 2 points: 14 students. 1 point: 6 students. 0 point: 13 students.
Problems in Mathematics of KöMaL, September 2005
