Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem B. 3844. (October 2005)

B. 3844. The legs of a right-angled triangle are a and b, its hypotenuse is c. The radius of the escribed circle drawn to the leg b (i.e. the one touching that leg on the outside and also touching the extensions of the other two sides) is \varrhob. Prove that b+c=a+2\varrhob.

(3 pont)

Deadline expired on November 15, 2005.

Sorry, the solution is available only in Hungarian. Google translation

Az ábra jelöléseivel élve OX=OY=OZ=\varrhoa. Az OXCY négyszögnek három szöge is derékszög, ezért az négyzet, vagyis CX=CY=\varrhoa. Az egybevágó OXB és OZB derékszögű háromszögekben BZ=BX=a-\varrhoa. AY=AZ miatt

2AY=AY+AZ=(b+\varrhoa)+(c+a-\varrhoa)=a+b+c,

ahonnan 2(b+\varrhoa)=a+b+c, vagyis b+2\varrhoa=a+c.

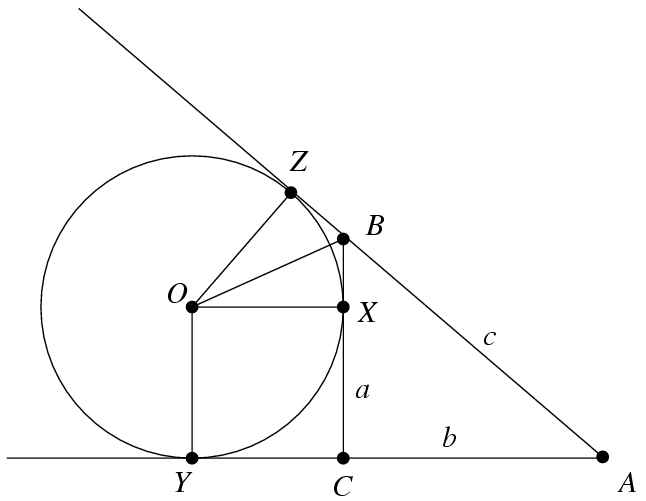
Statistics:

313 students sent a solution.
3 points:211 students.
2 points:83 students.
1 point:10 students.
0 point:7 students.
Unfair, not evaluated:2 solutionss.

Problems in Mathematics of KöMaL, October 2005