 Problem B. 3851. (October 2005)
Problem B. 3851. (October 2005)
B. 3851. Consider the functions obtained as compositions of the functions ,
, each used a finite number of times; for example
. Is it possible to obtain the function x
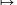 x+1 in this way? (It is allowed to cancel finitely many numbers from its domain.)
x+1 in this way? (It is allowed to cancel finitely many numbers from its domain.)
(5 pont)
Deadline expired on November 15, 2005.
Sorry, the solution is available only in Hungarian. Google translation
1. Megoldás: Nevezzük az f1, f2 f Nevezzük az f1, f2 függvényeket lényegében egyenlőnek, jelölésben f1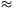 f2, ha mindkét függvény véges sok helytől eltekintve értelmezhető az egész számegyenesen és f1(x)=f2(x) teljesül minden olyan x-re, amely eleme mindkét függvény értelmezési tartományának. Az x
f2, ha mindkét függvény véges sok helytől eltekintve értelmezhető az egész számegyenesen és f1(x)=f2(x) teljesül minden olyan x-re, amely eleme mindkét függvény értelmezési tartományának. Az x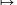 x függvényt jelölje id. A h2=hoh, és némi pongyolasággal a h(x)=h jelöléseket is alkalmazva ekkor
x függvényt jelölje id. A h2=hoh, és némi pongyolasággal a h(x)=h jelöléseket is alkalmazva ekkor
Innen már levezethető, hogy a két függvény véges sok példányának kompozíciójaként előállítható függvények bármelyike lényegében megegyezik az
függvények valamelyikével, hiszen ilyen alakra hozhatjuk az alábbi lépések segítségével, melyek mindegyike csökkenti a kompozícióban felírt függvények számát. Először is, ha egymás után kétszer szerepel az f, vagy háromszor a g függvény, akkor azt elhagyjuk a sorozatból, ha pedig valahol fogog jelenik meg, azt kicseréljük gof-re. Ilyen módon elérhetjük, hogy nem szerepel kétszer egymás után az f függvény, és a g sem, legfeljebb a legelején. Ezután pedig még elhagyhatjuk az olyan részeket is, ahol négyszer szerepel egymás után felváltva a két függvény. Mármost, ha a p=x+1 függvény ezek közül valamelyikkel lényegében egyenlő lenne, akkor ugyanez teljesülne a p2=x+2, p3=x+3 és általában a pi=x+i függvényre is, minden i természetes szám esetén. Ez azonban már végtelen sok páronként lényegében különböző függvény. Ezért a p függvényt nem lehet előállítani a megjelölt módon.
Megjegyzés. Egy kis további számolás azt is mutatja, hogy a fenti 10 függvény között csak 6 lényegesen különböző van: id,g,g2,f,gof,g2of. Ha a lényegében egyenlő függvényeket egymással azonosítjuk - megtehetjük, hiszen ekvivalenciarelációról van szó -, akkor a kompozíció műveletére nézve ez a 6 függvény egy csoportot alkot, amit azonosíthatunk egy szabályos háromszög szimmetriáinak csoportjával. Ha feltesszük magunknak a kérdést, hogyan lehetséges szorosabb kapcsolatot találni ezen függvények és a háromszög egybevágóságai között, és a háromszög csúcsait egy-egy valós számmal próbáljuk reprezentálni, akkor már az alábbi `egysoros' megoldásra is rájöhetünk különösebb isteni szikra nélkül.
2. Megoldás: Mind az f, mind a g függvény saját magára képezi a {-1,1/2,2} halmazt, ezért ugyanez történik bármely olyan függvény esetében, amely véges sok példányuk kompozíciójaként előállítható. Minthogy az r=x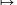 x+1 függvényre ez nem teljesül, az nem is állítható elő. Ebből sajnos az még nem olvasható le azonnal, hogy ez akkor is így lenne, ha az r függvény értelmezési tartományából nem csak a 0 és 1 helyeket hagyjuk el (ahol f,g, illetve az ezek kompozíciójával értelmezhető függvények esetleg nincsenek értelmezve). Ezen úgy segíthetünk, ha tetszőleges a
x+1 függvényre ez nem teljesül, az nem is állítható elő. Ebből sajnos az még nem olvasható le azonnal, hogy ez akkor is így lenne, ha az r függvény értelmezési tartományából nem csak a 0 és 1 helyeket hagyjuk el (ahol f,g, illetve az ezek kompozíciójával értelmezhető függvények esetleg nincsenek értelmezve). Ezen úgy segíthetünk, ha tetszőleges a 0,1 esetén tekintjük az
0,1 esetén tekintjük az számokból álló halmazt. Egy ilyen halmazra is igaz, hogy mind f, mind g, valamint ezek kompozíciói is a halmazt önmagára képezik. Ha r értelmezési tartományából csak véges sok elemet hagyunk el, akkor valamely a-ra az értelmezési tartomány még tartalmazni fog egy ilyen halmazt, amit azonban r nem képezhet önmagára.
Statistics:
82 students sent a solution. 5 points: 58 students. 4 points: 9 students. 3 points: 5 students. 2 points: 3 students. 1 point: 4 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, October 2005
