 Problem B. 3858. (November 2005)
Problem B. 3858. (November 2005)
B. 3858. There are traffic lights at eight junctions along a main road. The probability that a certain light is red when one arrives there is 0.4. What is the probability that a car travelling down the road is not stopped by red lights at two consecutive junctions?
(4 pont)
Deadline expired on December 15, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Legyen p=0,4 és q=1-p=0,6. Annak a valószínűsége, hogy utunk során valamilyen rögzített sorrendben a 8 darab piros lámpával és 8-a=b számú zölddel találkozunk, paqb. Ha nem találkozunk egymás után két tilos jelzéssel, akkor biztosan a
8 darab piros lámpával és 8-a=b számú zölddel találkozunk, paqb. Ha nem találkozunk egymás után két tilos jelzéssel, akkor biztosan a 4. Vizsgáljuk meg, hogy a egyes értékei esetén hány különböző sorrendben fordulhat ez elő. Ha a=0, akkor adott a sorrend: minden lámpa zöldet jelez. Ha a=1, akkor az egyetlen tilos jelzés 8 különböző helyen fordulhat elő. Ha a=4, akkor a zöld és piros lámpák felváltva kell, hogy egymást kövessék azzal a megjegyzéssel, hogy valahol lehet egymás után két zöld, ez öt lehetőség. Ha a=2, akkor a különböző lehetőségek száma 6+5+4+3+2+1=21=h(6), ahol h(n) az n-edik háromszög-számot jelöli. Ugyanis ha először az i-edik lámpánál kapunk pirosat (1
4. Vizsgáljuk meg, hogy a egyes értékei esetén hány különböző sorrendben fordulhat ez elő. Ha a=0, akkor adott a sorrend: minden lámpa zöldet jelez. Ha a=1, akkor az egyetlen tilos jelzés 8 különböző helyen fordulhat elő. Ha a=4, akkor a zöld és piros lámpák felváltva kell, hogy egymást kövessék azzal a megjegyzéssel, hogy valahol lehet egymás után két zöld, ez öt lehetőség. Ha a=2, akkor a különböző lehetőségek száma 6+5+4+3+2+1=21=h(6), ahol h(n) az n-edik háromszög-számot jelöli. Ugyanis ha először az i-edik lámpánál kapunk pirosat (1 i
i 6), akkor a második piros jelzésre 7-i különböző helyen kerülhet sor. Ez a gondolat azt is mutatja, hogy a=3 esetén, ha először az i-edik lámpánál kapunk tilosat (1
6), akkor a második piros jelzésre 7-i különböző helyen kerülhet sor. Ez a gondolat azt is mutatja, hogy a=3 esetén, ha először az i-edik lámpánál kapunk tilosat (1 i
i 4), akkor a további két piros lámpára összesen h(5-i) különböző helyen kerülhet sor. összesen tehát h(4)+h(3)+h(2)+h(1)=10+6+3+1=20 különböző sorrendben kaphatunk három tilos jelzést. Ezek alapján a keresett valószínűség
4), akkor a további két piros lámpára összesen h(5-i) különböző helyen kerülhet sor. összesen tehát h(4)+h(3)+h(2)+h(1)=10+6+3+1=20 különböző sorrendben kaphatunk három tilos jelzést. Ezek alapján a keresett valószínűség
q8+8pq7+21p2q6+20p3q5+5p4q4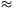 0,38.
0,38.
Statistics:
158 students sent a solution. 4 points: 82 students. 3 points: 35 students. 2 points: 8 students. 1 point: 11 students. 0 point: 21 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, November 2005
