 Problem B. 3865. (December 2005)
Problem B. 3865. (December 2005)
B. 3865. The triangles AB1C1 and AB2C2 are similar, and their vertices are labelled in the same direction around the triangle. The lines B1B2 and C1C2 intersect at the point D. (a) Show that the triangles AB1B2 and AC1C2 are similar. (b) Show that the circumscribed circles of AB1C1 and AB2C2 pass through the point D.
(4 pont)
Deadline expired on January 16, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Mivel A D, a B1,A,B2 pontok nem esnek egy egyenesre, csakúgy, mint a C1,A,C2 pontok. A szóban forgó háromszögek tehát léteznek. Vegyük az eredeti háromszögek körüljárási irányát pozitívnak. Szükség esetén az indexeket felcserélve, feltehetjük, hogy az AB1C1 háromszöget A körüli
D, a B1,A,B2 pontok nem esnek egy egyenesre, csakúgy, mint a C1,A,C2 pontok. A szóban forgó háromszögek tehát léteznek. Vegyük az eredeti háromszögek körüljárási irányát pozitívnak. Szükség esetén az indexeket felcserélve, feltehetjük, hogy az AB1C1 háromszöget A körüli  szögű forgatva nyújtás viszi az AB2C2 háromszögbe, ahol 0<
szögű forgatva nyújtás viszi az AB2C2 háromszögbe, ahol 0< <
< . Legyen a B1AC1 és B2AC2 irányított szögek nagysága
. Legyen a B1AC1 és B2AC2 irányított szögek nagysága  , továbbá a hasonlóság miatt
, továbbá a hasonlóság miatt
C1A/B1A=C2A/B2A=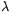 .
.
Ekkor az AB1B2 háromszöget A körüli  szöggel történő,
szöggel történő, 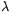 arányú forgatva nyújtás viszi az AC1C2 háromszögbe, ami az első állí tást igazolja. Ugyanez a forgatva nyújtás az ábrán feltüntetett b=B1B2 irányított egyenest a c=C1C2 irányított egyenesbe viszi. Ezeket a D pont két részre osztja, melyeket nevezzünk értelemszerűen bal-, illetve jobboldali résznek.
arányú forgatva nyújtás viszi az AC1C2 háromszögbe, ami az első állí tást igazolja. Ugyanez a forgatva nyújtás az ábrán feltüntetett b=B1B2 irányított egyenest a c=C1C2 irányított egyenesbe viszi. Ezeket a D pont két részre osztja, melyeket nevezzünk értelemszerűen bal-, illetve jobboldali résznek.
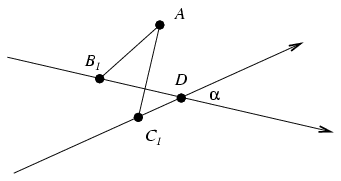
A második állítás igazolásához vegyük figyelembe, hogy az AB1B2 és AC1C2 háromszögek körüljárási iránya is pozitív. Szimmetria okok miatt elegendő azt bizonyítani, hogy az A,B1,C1 és D pontok egy körön vannak. Ez nyilvánvaló, ha B1 vagy C1 egybeesik D-vel. Az nem lehet, hogy B1 a b egyenes jobboldali részén és ugyanakkor C1 pedig a c egyenes baloldali részén helyezkedik el, ekkor ugyanis az AB1C1 háromszög negatív körüljárású lenne. Ennek alapján 3 esetet különböztethetünk meg. Az ábrán látható első esetben mindkét pont a megfelelő egyenes baloldali részén helyezkedik el. Ekkor az A és D pontok a B1C1 egyenesnek ugyanazon oldalára esnek, és a B1C1 szakasz mindkettőből  szög alatt látszik, vagyis az állítás következik a kerületi szögek tételének megfordí tásából. Hasonló a helyzet abban az esetben is, ha mindkét pont a megfelelő irányított egyenes jobboldalán van. Végül ha B1 a b baloldalán, C1 pedig c jobboldali részén van, akkor a B1C1 egyenes elválasztja az A és D pontokat. Ekkor azonban a B1C1 szakasz D-ből
szög alatt látszik, vagyis az állítás következik a kerületi szögek tételének megfordí tásából. Hasonló a helyzet abban az esetben is, ha mindkét pont a megfelelő irányított egyenes jobboldalán van. Végül ha B1 a b baloldalán, C1 pedig c jobboldali részén van, akkor a B1C1 egyenes elválasztja az A és D pontokat. Ekkor azonban a B1C1 szakasz D-ből  -
- szög alatt látszik, vagyis az AB1DC1 négyszög húrnégyszög.
szög alatt látszik, vagyis az AB1DC1 négyszög húrnégyszög.
Statistics:
168 students sent a solution. 4 points: Anda Roland, Balambér Dávid, Bogár 560 Péter, Bus Norbert, Csaba Ákos, Csima Géza, Csorba János, Gaál Zsuzsanna, Gaizer Tünde, Gresits Iván, Gyüre Balázs, Klimaj Zoltán, Kovács 129 Péter, Kristóf Panna, Kunovszki Péter, Lovász László Miklós, Mercz Béla, Nagy-Baló András, Németh Kitti Noémi, Pálovics Róbert, Peregi Tamás, Prőhle Zsófia, Salát Zsófia, Ta Phuong Linh, Tossenberger Anna, Udvari Balázs, Vajsz Tibor, Véges Márton. 3 points: 81 students. 2 points: 28 students. 1 point: 23 students. 0 point: 8 students.
Problems in Mathematics of KöMaL, December 2005
