Problem B. 3869. (December 2005)

B. 3869. Point M lies on the angle bisector drawn from vertex A, inside an acute-angled triangle ABC. The other intersections of the lines AM, BM, CM with the circumscribed circle are A₁, B₁ and C₁, respectively. The lines AB and C₁A₁ intersect at L, and the lines AC and B₁A₁ intersect at N. Prove that LN is parallel to BC.

(5 pont)

Deadline expired on January 16, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Mivel AA₁ felezi a BAC szöget, a BA₁ és CA₁ ívek egyenlők. A kerületi szögek tétele alapján tehát a mellékelt ábrán számos egymással egyenlő szöget fedezhetünk fel. Így például

$CB_1N\sph=CAM\sph=A_1C_1M\sph,\quad B_1CN\sph=B_1A_1M\sph=MBA\sph$

és

$ACM\sph=C_1A_1M\sph=C_1BA\sph.$

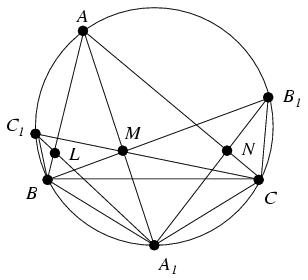
Ezért az NCB₁ háromszög hasonló az MA₁B₁ háromszöghöz, amiért is NC/MA₁=B₁C/B₁A₁, továbbá AC/AM=C₁A₁/C₁M is leolvasható az ACM és C₁A₁M háromszögek hasonlóságából. A két egyenlőséget összevetve kapjuk, hogy

${NC\over MA_1}:{AC\over AM}={B_1C\over A_1B_1}:{A_1C_1\over MC_1}.$

Ugyanígy kapjuk szimmetria okok miatt az

${LB\over MA_1}:{AB\over AM}={C_1B\over A_1C_1}:{A_1B_1\over MB_1}$

egyenlőséget. A két egyenlőséget egymással elosztva kapjuk, hogy

${NC\over AC}:{LB\over AB}={B_1C\over MB_1}:{C_1B\over MC_1}.$

Mármost $CB_1M\sph=BC_1M\sph$ és

$C_1BM\sph=C_1BA\sph+MBA\sph=ACM\sph+B_1CN\sph=B_1CM\sph$

miatt a C₁BM és B₁CM háromszögek is hasonlók, vagyis a jobboldalon álló arány 1-gyel egyenlő. Ezért NC/AC=LB/AB, és a párhuzamos szelők tételének megfordítása adja a bizonyítandó állítást.

Statistics:

59 students sent a solution.

5 points: 55 students.

4 points: 1 student.

2 points: 1 student.

0 point: 2 students.

Problems in Mathematics of KöMaL, December 2005

59 students sent a solution.
5 points:	55 students.
4 points:	1 student.
2 points:	1 student.
0 point:	2 students.

Already signed up?
New to KöMaL?