Problem B. 3884. (February 2006)

B. 3884. Three unit circles all pass through the point P. Their other intersections are A, B and C. Find the radius of the circumscribed circle of the triangle ABC.

(4 pont)

Deadline expired on March 16, 2006.

Sorry, the solution is available only in Hungarian. Google translation

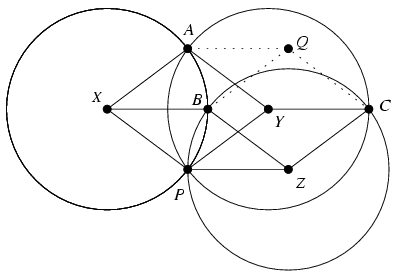
Megoldás: Jelölje a körök középpontját X,Y és Z az ábra szerint. Ekkor a PXAY, PXBZ és PYCZ négyszögek egyaránt egység oldalhosszúságú rombuszok, amiértis $\ora{XA}=\ora{PY}=\ora{ZC}$ . Legyen Q az a pont, amelyre $\ora{AQ}=\ora{XB}$ , ekkor $\ora{BQ}=\ora{XA}$ , vagyis $\ora{BQ}=\ora{ZC}$ , tehát $\ora{CQ}=\ora{ZB}$ is igaz. Beláttuk tehát, hogy az $\ora{AQ}$ , $\ora{BQ}$ és $\ora{CQ}$ vektorok mindegyike egység hosszú, vagyis az A,B,C pontok egyránt egységnyi távolságra helyezkednek el a Q ponttól. Az ABC háromszög köré írható kör középpontja ezek szerint a Q pont, sugara pedig egységnyi.

Statistics:

125 students sent a solution.

4 points: 63 students.

3 points: 39 students.

2 points: 8 students.

1 point: 10 students.

0 point: 2 students.

Unfair, not evaluated: 3 solutionss.

Problems in Mathematics of KöMaL, February 2006

125 students sent a solution.
4 points:	63 students.
3 points:	39 students.
2 points:	8 students.
1 point:	10 students.
0 point:	2 students.
Unfair, not evaluated:	3 solutionss.

Already signed up?
New to KöMaL?