 Problem B. 3886. (February 2006)
Problem B. 3886. (February 2006)
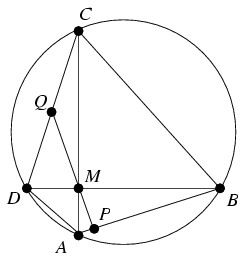
B. 3886. The diagonals of a cyclic quadrilateral ABCD are perpendicular. A perpendicular is dropped from the intersection of the diagonals onto the line AB. In what ratio does the perpendicular divide the side CD?
(4 pont)
Deadline expired on March 16, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Legyen az átlók M metszéspontjából az AB egyenesre állított merőleges talppontja P, a CD oldallal alkotott metszéspontja pedig Q. A kerületi szögek tétele miatt a BAC és BDC szögek egyenlők, vagyis a PAM és MDC derékszögű háromszögek hasonlók. Továbbá a PMA és CMQ szögek váltószögek, melyek közül az utóbbit a QMD szög derékszögre egészíti ki, akárcsak az MCQ szöget a QDM szög. Ennélfogva a QMC és QDM háromszög is egyenlő szárú, QC=QM=QD, tehát a Q pont felezi a CD oldalt.
Statistics:
167 students sent a solution. 4 points: 140 students. 3 points: 17 students. 2 points: 2 students. 1 point: 1 student. 0 point: 5 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, February 2006
