 Problem B. 3895. (March 2006)
Problem B. 3895. (March 2006)
B. 3895. The edges of a square based right prism are a=b=8, c=27 units long. Cut the prism into four parts, such that it is possible to put them together to form a cube.
(5 pont)
Deadline expired on April 18, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Egy x×y méretű tégalapot szét tudunk vágni az ábrán látható módon két részre úgy, hogy azokból egy 2x/3×3y/2 méretű téglalapot lehessen összerakni. Ennek alapján egy x×y×z méretű téglatest is szétvágható két részre úgy, hogy azokból egy 2x/3×3y/2×z méretű téglatestet lehessen összerakni. Az egyes dimenziók szerepe természetesen teljesen szimmetrikus.
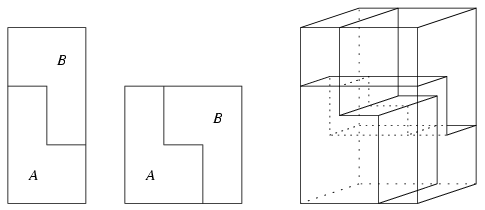
Ennek alapján így járhatunk el. Az ismertetett módon a 8×8×27-es téglatestet először két részre vágjuk, és azokból összerakunk egy 12×8×18-as téglatestet. Ezt megint két részre vágjuk, és azokból összerakunk egy most már 12×12×12 méretű kockát. Azt kell még meggondolni, hogy a második szétvágás során az első vágás után keletkezett részek külön-külön két részre esnek szét. Ábránkon a 12×8×18-as téglatest szétvágását próbáltuk meg szemléltetni négy olyan részre, amelyekből mind a 8×8×27, mind pedig a 12×12×12 méretű téglatest összerakható.
Statistics:
17 students sent a solution. 5 points: Dombi Soma, Fegyverneki Tamás, Honner Balázs, Kiskovács Ágnes, Mészáros Gábor, Páldy Sándor, Peregi Tamás, Pirkó Dániel, Sümegi Károly, Szalóki Dávid, Szilágyi 987 Csaba, Tálosi András, Tossenberger Anna, Udvari Balázs. 0 point: 3 students.
Problems in Mathematics of KöMaL, March 2006
