 Problem B. 3898. (March 2006)
Problem B. 3898. (March 2006)
B. 3898. It is known that the line segments connecting the midpoints of the opposite edges of a tetrahedron are concurrent. Is it possible to select a point on each edge that divides the edge 1:2, such that the line segments connecting the selected points of opposite edges are concurrent?
(3 pont)
Deadline expired on April 18, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás:
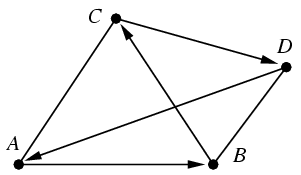
A tetraéder két szemközti élét elhagyva, a megmaradt négy él által alkotott zárt töröttvonalon irányítsuk meg körbe az éleket az ábra szerint. Ha egy irányított élről az első harmadolópontot választottuk, akkor ahhoz rendeljünk egyet, ha a másodikat, akkor pedig kettőt. Ha az ábrán látható irányí tott körön végighaladva egy vagy három alkalommal szerepel az osztópontok mellett 1, akkor a négy pont nincs egy síkban, a hozzájuk tartozó két összekötő szakasz tehát nem metszheti egymást. Vagyis a két szakasz csak akkor mehet át egy ponton, ha az irányított körön végighaladva a számok összege páros. Ha egy él irányát megváltoztatjuk, az összeg paritása is megváltozik.
Tegyük fel, hogy a harmadolópontokat úgy választottuk meg, hogy az összekötő szakaszok egy ponton mennek át. Az e élen lévő számot f(e)-vel jelölve tehát p=f(AB)+f(BC)+f(CD)+f(AD) páros szám. Irányítsuk meg a fennmaradó két élet B-től D felé, illetve A-tól C felé. Az ABDC körön végighaladva két élen haladunk az irányítással ellentétes irányba, vagyis q=f(AB)+f(BD)+f(CD)+f(AC) is páros szám. Az ACBD körön viszont csak egyszer haladunk az irányítással ellentétes irányba, tehát r=f(AC)+f(BC)+f(BD)+f(AD) páratlan.
Ekkor p+q+r egyrészt páratlan, másrészt pedig páros, hiszen benne minden f(e) összeadandó pontosan kétszer szerepel. Ez az ellentmondás mutatja, hogy az osztópontokat nem lehet a kívánt módon kiválasztani.
Statistics:
23 students sent a solution. 3 points: Anda Roland, Balambér Dávid, Bartha Zsolt, Beck Zoltán, Blázsik Zoltán, Csaba Ákos, Cserép Máté, Duba Zsombor, Elekes Csaba, Herber Máté, Kristóf Panna, Nagy 235 János, Nagy-Baló András, Németh Kitti Noémi, Salát Zsófia, Sümegi Károly, Tolner Ferenc, Tomon István, Vajsz Tibor. 2 points: Pap Bálint, Szabó Levente. 0 point: 2 students.
Problems in Mathematics of KöMaL, March 2006
