 Problem B. 3902. (April 2006)
Problem B. 3902. (April 2006)
B. 3902. P is an interior point of the triangle ABC. The perimeter of the triangle is 2s. Show that s<PA+PB+PC<2s.
(3 pont)
Deadline expired on May 18, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Az ABP, BCP és CAP háromszögekre felírva a háromszög egyenlőtlenséget az
egyenlőtlenségekhez jutunk. Ezeket összegezve, majd a kapott egyenlőtlenséget 2-vel osztva s<PA+PB+PC adódik.
A másik egyenlőtlenség bizonyításához húzzunk párhuzamost a P ponton át az AB egyenessel, ennek az oldalakkal vett metszéspontjait jelölje A' és B' az ábra szerint.
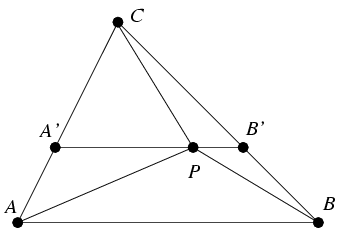
Most AP<AA'+A'P és BP<BB'+B'P alapján
AP+BP<(AA'+BB')+(A'P+PB')=(AA'+BB')+A'B'<(AA'+BB')+AB.
Továbbá CP<A'C+B'C is igaz, hiszen CP rövidebb az A'C és B'C szakaszok valamelyikénél. Következésképpen
PA+PB+PC<(AA'+A'C)+(BB'+B'C)+AB=2s.
Statistics:
139 students sent a solution. 3 points: 127 students. 2 points: 5 students. 1 point: 7 students.
Problems in Mathematics of KöMaL, April 2006
