Problem B. 3909. (April 2006)

B. 3909. A fair coin is tossed 12 times in a row and the outcomes are listed. What is the probability that there are no three consecutive heads?

(5 pont)

Deadline expired on May 18, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Az n dobásból álló 2ⁿ számú lehetséges sorozat közül - melyek mindegyike ugyanolyan p(n)=1/2ⁿ valószínűséggel következik be - jelölje A(n) azoknak a számát, amelyekben nincs három egymást követő fej. Ezen belül jelölje A₀(n) azon sorozatok számát, amelyekben az utolsó dobás írás, A₁(n) és A₂(n) pedig azokét, ahol az utolsó két dobás rendre írás-fej, illetve fej-fej. Könnyen meggondolhatjuk, hogy A(1)=2, A(2)=4 és A(3)=7. Világos, hogy minden n-re

$A_0(n+1)=A(n)\quad \hbox{\rm \'es}\quad A_1(n+1)=A_0(n),$

valamint n $\ge$ 2 esetén

$A(n)=A_0(n)+A_1(n)+A_2(n)\quad \hbox{\rm \'es}\quad A_2(n+1)=A_1(n).$

Következésképpen minden n-re érvényes az

A(n+3)=A₀(n+3)+A₁(n+3)+A₂(n+3)=A(n+2)+A₀(n+2)+A₁(n+2)=

=A(n+2)+A(n+1)+A₀(n+1)=A(n+2)+A(n+1)+A(n)

összefüggés, amelynek segítségével A(12) értékét könnyen kiszámolhatjuk:

$A(4)=13,\ A(5)=24,\ A(6)=44,\ A(7)=81,\ A(8)=149,\ A(9)=274,$

$\ A(10)=504,\ A(11)=927, \quad \hbox{\rm \'es v\'eg\"ul}\quad A(12)=1705.$

A keresett valószínűség tehát

p(12)A(12)=1705/4096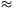 $\approx$ 0,416.

Statistics:

75 students sent a solution.

5 points: 52 students.

4 points: 3 students.

3 points: 7 students.

2 points: 4 students.

1 point: 4 students.

0 point: 4 students.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, April 2006

75 students sent a solution.
5 points:	52 students.
4 points:	3 students.
3 points:	7 students.
2 points:	4 students.
1 point:	4 students.
0 point:	4 students.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?