 Problem B. 3914. (May 2006)
Problem B. 3914. (May 2006)
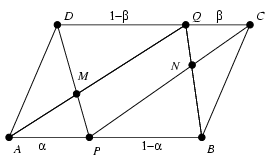
B. 3914. P is an arbitrary point on the side AB of the parallelogram ABCD, and Q is an arbitrary point of side CD. Let M denote the intersection of the lines DP and AQ, and let N denote the intersection of the lines CP and BQ. Show that the line MN is passing through the centre of the parallelogram.
(4 pont)
Deadline expired on June 15, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Vezessük be azt az általános jelölést, hogy a paralelogramma O középpontjából az X csúcsba az x vektor mutat. Ekkor c=-a és d=-b. Tegyük fel, hogy a P pont az AB szakaszt  :1-
:1- , a Q pont pedig a CD szakaszt
, a Q pont pedig a CD szakaszt  :1-
:1- arányban osztja. Ekkor p=(1-
arányban osztja. Ekkor p=(1- )a+
)a+ b, és AP:QD=
b, és AP:QD= :1-
:1- .
.
A párhuzamos szelők tétele miatt az M pont a PD szakaszt ugyanilyen arányban osztja, vagyis
A jelölések szimmetriáját felhasználva számolás nélkül is láthatjuk, hogy
Az m,n vektorok tehát párhuzamosak, vagyis az O,M,N pontok valóban egy egyenesre esnek.
Statistics:
41 students sent a solution. 4 points: Almási 270 Gábor András, Balambér Dávid, Blázsik Zoltán, Bogár 560 Péter, Csaba Ákos, Cseh Ágnes, Cséke Balázs, Cserép Gergely, Dányi Zsolt, Farkas Ádám László, Herber Máté, Honner Balázs, Károlyi Márton, Kiss 111 Viktor, Kovács 111 Péter, Kovács 129 Péter, Mercz Béla, Mészáros Gábor, Nagy 235 János, Nagy 314 Dániel, Németh 007 Zsolt, Páldy Sándor, Peregi Tamás, Prőhle Zsófia, Salát Zsófia, Sárkány Lőrinc, Szabó 108 Tamás, Szalkai Balázs, Szalóki Dávid, Szirmai Péter, Szűcs Gergely, Ta Phuong Linh, Tallián György, Tossenberger Anna, Udvari Balázs, Véges Márton, Zieger Milán. 3 points: Pásztor Attila, Szilágyi 987 Csaba. 1 point: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, May 2006
