 Problem B. 3923. (September 2006)
Problem B. 3923. (September 2006)
B. 3923. A diagonal is drawn in a few fields of a chessboard, such that no two of them have a common point. What is the maximum possible number of diagonals that can be drawn in this way?
(Based on a problem of the Zrínyi Competition)
(4 pont)
Deadline expired on October 16, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: 36 átlót megrajzolhatunk az ábrán látható módon.
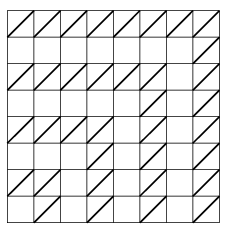
Ennél többet azonban nem, ugyanis a sakktábla mezőinek csúcsai egy 9×9-es rácsot alkotnak, minden berajzolható átlónak valamelyik végpontja ezen rács 2., 4., 6. vagy 8. sorában helyezkedik el, és ezen 36 pont mindegyike legfeljebb egy berajzolt átlóhoz tartozhat.
Statistics:
320 students sent a solution. 4 points: 86 students. 3 points: 41 students. 2 points: 136 students. 1 point: 2 students. 0 point: 53 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, September 2006
