B. 3923. A sakktábla néhány mezőjének behúzzuk egy-egy átlóját úgy, hogy semelyik kettőnek ne legyen közös pontja. Legfeljebb hány átlót rajzolhatunk így meg?

(Zrínyi versenyfeladat nyomán)

(4 pont)

A beküldési határidő LEJÁRT.

Megoldás: 36 átlót megrajzolhatunk az ábrán látható módon.

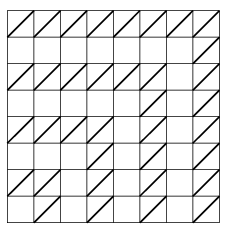
Ennél többet azonban nem, ugyanis a sakktábla mezőinek csúcsai egy 9×9-es rácsot alkotnak, minden berajzolható átlónak valamelyik végpontja ezen rács 2., 4., 6. vagy 8. sorában helyezkedik el, és ezen 36 pont mindegyike legfeljebb egy berajzolt átlóhoz tartozhat.

A B. 3923. feladat statisztikája 320 dolgozat érkezett. 4 pontot kapott: 86 versenyző. 3 pontot kapott: 41 versenyző. 2 pontot kapott: 136 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 53 versenyző. Nem versenyszerű: 2 dolgozat.