 Problem B. 3930. (September 2006)
Problem B. 3930. (September 2006)
B. 3930. Prove that by drawing some noncrossing diagonals it can be divided into triangles such that each vertex of the polygon belongs to an odd number of them.
(4 pont)
Deadline expired on October 16, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Legyen a sokszög csúcsainak száma 3k, ahol k pozitív egész. Az állítást k szerinti teljes indukcióval igazoljuk. Ha k=1, akkor az állítás nyilvánvaló. Legyen tehát k 2, és tegyük fel, hogy bármely 3(k-1) csúcsú konvex sokszög háromszögekre bontható a kívánt módon. Tekintsünk egy
2, és tegyük fel, hogy bármely 3(k-1) csúcsú konvex sokszög háromszögekre bontható a kívánt módon. Tekintsünk egy konvex sokszöget. A
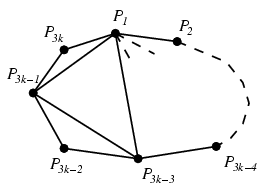
sokszögnek húzzuk be néhány átlóját az indukciós feltevésnek megfelelő módon, ezek egyben a K sokszögnek is átlói. Ezeken kívül húzzuk még be K-ban a P1P3k-3, a P1P3k-1 és P3k-3P3k-1 átlókat. Így K-t is felbontottuk háromszögekre. Ez megfelelő lesz, ugyanis a
csúcsokra ugyanannyi háromszög illeszkedik, mint K' felbontásában, a P1 és P3k-3 pontokra 2-vel több (tehát ugyancsak páratlan sok), a P3k-2, illetve P3k csúcsokra egy-egy, P3k-1-re pedig 3.
Statistics:
176 students sent a solution. 4 points: 146 students. 3 points: 12 students. 2 points: 1 student. 1 point: 2 students. 0 point: 13 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, September 2006
