Problem B. 3934. (October 2006)

B. 3934. A rectangle and two squares are drawn inside a right-angled triangle shown in the figure. Prove that the height of the rectangle is equal to the sum of heights of the squares.

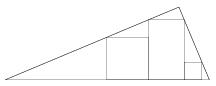
(3 pont)

Deadline expired on November 15, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az ábrán látható derékszögű háromszögek egymáshoz hasonlóak. A párhuzamos szelők tétele miatt AA'/BB'=AC/BC, ugyanígy aránylanak tehát egymáshoz a kis négyzetek odalai: A''X/ZB''=AC/BC, és az A'A''Y háromszög befogói is: A''Y/A'Y=AC/BC. Ezért A''X=A''Y miatt A'Y=ZB'', ahonnan a téglalap magassága A''X+A'Y=A''X+ZB'', amint azt bizonyítani akartuk.

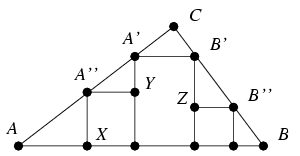
Statistics:

257 students sent a solution.
3 points:	239 students.
2 points:	12 students.
1 point:	2 students.
0 point:	2 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, October 2006