Problem B. 3939. (October 2006)

B. 3939. Find the angle encompassed by the hypotenuse of a right-angled triangle with circumference of 2 units, as seen from a point lying on the inner angle bisector of the right angle at a distance of $\sqrt{2}$ from that vertex.

(4 pont)

Deadline expired on November 15, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az ábra jelöléseit használva a+b+c=2 és a²+b²=c², ahonnan a²+b²=(2-a-b)², vagyis ab=2a+2b-2. Az ACD, illetve BCD háromszögekre a koszinusz-tételt felírva kapjuk, hogy

u²=b²-2b+2, v²=a²-2a+2.

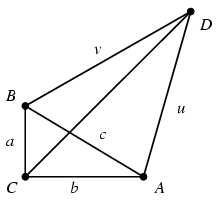
Ezért

u²v²=a²b²-2a²b-2ab²+4ab-4a-4b+4+2a²+2b²=

=a²b²-2ab(a+b)+4ab-2ab+2c²=ab(ab-2a-2b+2)+2c²=2c²,

ahonnan az ADB szög koszinuszára

$\frac{u^2+v^2-c^2}{2uv}=\frac{4-2a-2b}{2uv}=\frac{c}{uv}=\frac{1}{\sqrt{2}}$

adódik. A háromszög átfogója tehát 45^o-os szög alatt látszik a D pontból.

Statistics:

139 students sent a solution.

4 points: 104 students.

3 points: 14 students.

2 points: 4 students.

1 point: 12 students.

0 point: 5 students.

Problems in Mathematics of KöMaL, October 2006

139 students sent a solution.
4 points:	104 students.
3 points:	14 students.
2 points:	4 students.
1 point:	12 students.
0 point:	5 students.

Already signed up?
New to KöMaL?