 Problem B. 3944. (November 2006)
Problem B. 3944. (November 2006)
B. 3944. Sketch in the cartesian plane the region consisting of the points (x,y) such that .
(3 pont)
Deadline expired on December 15, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Nyilván sem x, sem y értéke nem lehet 0. Közös nevezőre hozva, majd átrendezve az egyenlőtlenség így alakul:
Tekintsük az y-x=0, x-1=0, y-1=0, x=0 és y=0 egyeneseket. Az f tört nem értelmezhető, ha a P(x,y) pont az utolsó két egyenes valamelyikére esik, és pontosan akkor 0 az f értéke, ha P az első három egyenes valamelyikére esik (de az utolsó kettő egyikére sem). Ennek alapján az első három egyenes három pontját kell kizárnunk.
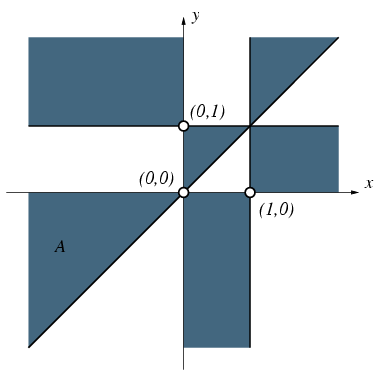
Az öt egyenes a síkot 12 részre osztja. Minden egyes ilyen nyílt tartományon belül az f tört előjele állandó. Pontosan akkor lesz f>0, ha az y-x, x-1, y-1, x és y kifejezések közül páratlan sok pozitív, a többi pedig negatív. Ez a helyzet például a III. síknegyed y=0 és y=x egyenesek által határolt A tartományában, ahol csak y-x értéke lesz pozitív, az összes többi negatív. Ha két tartománynak van közös (véges vagy végtelen hosszú) határoló szakasza, akkor az egyiken pozitív, a másikon pedig negatív lesz f értéke. Ezek alapján a szóban forgó pontokan könnyen ábrázolhatjuk az A tartományból kiindulva.
Statistics:
157 students sent a solution. 3 points: 57 students. 2 points: 56 students. 1 point: 30 students. 0 point: 13 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, November 2006
