 Problem B. 3949. (November 2006)
Problem B. 3949. (November 2006)
B. 3949. For what values of the positive integer n is there a simple graph in which the degree of each vertex is at most n, and there are i vertices of degree i for all 1 i
i n?
n?
(Suggested by G. Mészáros, Kemence)
(4 pont)
Deadline expired on December 15, 2006.
Sorry, the solution is available only in Hungarian. Google translation
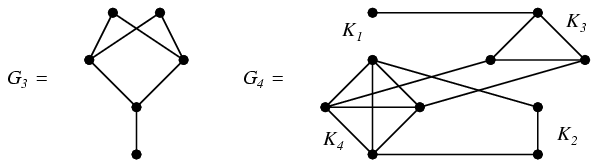
Megoldás. A fokszámok n(n+1)/2 összege, lévén az élek számának kétszerese, páros szám kell legyen. Ezért szükséges, hogy az n szám 4-gyel osztva 0 vagy 3 maradékot adjon. Megmutatjuk, hogy ez a feltétel egyben elégséges is. Az n=3, illetve az n=4 esetben ilyen gráfot láthatunk a mellékelt ábrán. Már csak azt kell megmutatni, hogy ha valamely n-re találtunk egy megfelelő Gn gráfot, akkor n értékét 4-gyel növelve, tudunk konstruálni egy megfelelő Gn+4 gráfot. Ezt pedig úgy tehetjük meg, ha a először a Gn gráf mellé felvesszük a Kn+1, Kn+2, Kn+3 és Kn+4 teljes gráfokat rendre n+1, n+2, n+3, illetve n+4 csúcson úgy, hogy az öt gráf csúcshalmazai páronként diszjunktak legyenek, majd pedig a Kn+1 és Kn+4 gráfok összesen 2n+5 csúcsát egy-egy új él segítségével összepárosítjuk a Kn+2 és Kn+3 gráfok összesen 2n+5 csúcsával. (Tulajdonképpen már a G4 gráfot is megkaphatjuk ilyen módon a 0 szögpontú G0 üres gráfból.)
Statistics:
89 students sent a solution. 4 points: Aczél Gergely, Ágoston Tamás, Anda Roland, Aujeszky Tamás, Bartha Zsolt, Blázsik Zoltán, Blutman Kristóf László, Bock Lilla, Bodor Bertalan, Bogár 560 Péter, Csaba Ákos, Cseh Ágnes, Cséke Balázs, Éles András, Fonyó Dávid, Gévay Gábor, Gresits Iván, Grósz Dániel, Győrffy Lajos, Herber Máté, Honner Balázs, Károlyi Gergely, Kiss 243 Réka, Kiss 902 Melinda Flóra, Kornis Kristóf, Korom-Vellás Judit, Kunos Ádám, Kunovszki Péter, Kurgyis Eszter, Mészáros András, Nagy 314 Dániel, Paál Gergely, Papp 648 Pál András, Peregi Tamás, Salát Zsófia, Sárkány Lőrinc, Sümegi Károly, Szalkai Balázs, Szalóki Dávid, Szűcs Gergely, Tallián György, Tossenberger Anna, Tóth 222 Barnabás, Tóth 666 László Márton, Tóth 796 Balázs, Török Balázs, Vajsz Tibor, Varga 171 László, Wolosz János. 3 points: 17 students. 2 points: 18 students. 1 point: 5 students.
Problems in Mathematics of KöMaL, November 2006
