Problem B. 3958. (December 2006)

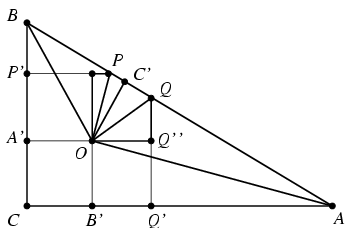
B. 3958. The triangle ABC is right angled at C and its incentre is O. The perpendiculars drawn at the point O to the line segments OA and OB meet the side AB at P and Q, respectively. The foot of the perpendicular from P to the side BC is P', and that from Q to the side AC is Q'. Prove that the points P', Q' and O are collinear.

(4 pont)

Deadline expired on January 15, 2007.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Legyen az O pont merőleges vetülete az AB,AC,BC és QQ' szakaszokra rendre C',B',A', illetve Q''. Ekkor OA'=OB'=OC'=r, ahol r a beírt kör sugara. A C'OQ és OBQ háromszögek hasonló derékszögű háromszögek, vagyis a C'OQ szög egyenlő az OBQ szöggel, ami éppen az ABC szög fele. Másrészt OC' merőleges AB-re és OQ'' merőleges BC-re, vagyis a C'OQ'' szög egyenlő az ABC szöggel. Ezért a QOQ'' szög is éppen az ABC szög felével egyenlő.

A C'OQ és Q''OQ derékszögű háromszögek ezért egybevágóak, vagyis OQ''=OC'=r, ahonnan kapjuk, hogy B'Q'=OQ''=r=OB', tehát az OB'Q' háromszög olyan egyenlőszárú derékszögű háromszög, amelynek befogója r. Hasonló állítás igaz az P'A'O háromszögre is. Mivel a két háromszög egymásnak megfelelő befogói páronként egymással párhuzamosak, az átfogók is azok lesznek, ami bizonyítja az állítást, sőt az is kiderül ebből, hogy az O pont éppen a P'Q' szakasz felezőpontja.

Statistics:

111 students sent a solution.
4 points:	100 students.
3 points:	4 students.
2 points:	2 students.
1 point:	1 student.
0 point:	2 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, December 2006