B. 3963. A counter is travelling from the lower left corner to the upper right corner of the chessboard. It moves either one field to the right or one field up in each step. How many routes are there that pass through at least one of the four fields at the centre?

(4 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás: Ha az útvonal áthalad a D mezőn, akkor vagy a B-n, vagy a C-n át kell haladnia. A B mezőre vagy az A-ról, vagy az E-ről léphet, a C-re pedig A-ról vagy F-ről. Azt kell tehát összeszámolni, hány olyan útvonal van, amely a) áthalad A-n, vagy b) áthalad E-n és B-n, vagy c) áthalad F-en és C-n. Ez az átfogalmazás azért hasznos, mert a három eset páronként kizárja egymást. Szimmetria okok miatt pedig a c) esetben pontosan ugyanannyi úvonalat számolhatunk össze, mint a b) esetben.

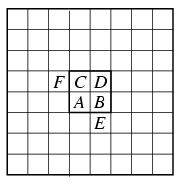
A bal alsó saroktól az A mezőig 6 lépés alatt juthatunk el, ebből pontosan 3-szor kell jobbra lépnunk (és 3-szor felfelé), erre tehát lehetőségünk van. Hasonlóképpen, ha az A-ból el szeretnénk jutni a jobb fölső sarokba, akkor az ehhez szükséges 8 lépésből pontosan 4-szer kell jobbra lépnünk, a lehetőségek száma tehát . Az a) esetben tehát 20^.70=1400 különböző útvonalat számolhatunk össze.

A b) esetre térve, a bal alsó sarokból E-be féleképp juthatunk el, innen át kell lépnünk B-re, onnan a jobb fölső sarokba pedig féleképpen haladhatunk tovább, vagyis összesen 15^.35 ilyen útvonal van, akárcsak a c) esetben.

Az összes lehetséges útvonal száma tehát

20^.70+2^.15^.35=35^.70=2450.

Statistics on problem B. 3963. 268 students sent a solution. 4 points: 217 students. 3 points: 15 students. 2 points: 10 students. 1 point: 8 students. 0 point: 16 students. Unfair, not evaluated: 2 solutions.