 Problem B. 3971. (January 2007)
Problem B. 3971. (January 2007)
B. 3971. The sum of the non-negative numbers x, y, z is 1. Let
What are the maximum possible values of S and C?
(5 pont)
Deadline expired on February 15, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Vizsgáljuk először az S értékét. Feltehetjük, hogy a számok közül z a legkisebb, ekkor c=1-z=x+y 2/3.
2/3.
S=cxy+(c2-2xy)(1-c)+c(1-c)2=(3c-2)xy+c(1-c).
Itt xy c2/4, ahol egyenlőség pontosan az x=y=c/2 esetben áll fenn. Ezért
c2/4, ahol egyenlőség pontosan az x=y=c/2 esetben áll fenn. Ezért
ahol egyenlőség pontosan az x=y=c/2 esetben áll fenn. A jobboldalon álló függvény c szerinti deriváltja
Az f(c) függvény tehát az egész számegyenesen szigorúan monoton nő, a 2/3 c
c 1 feltétel mellett tehát legnagyobb értékét a c=1 helyen veszi fel. Ezek alapján S lehetséges legnagyobb értéke Smax =f(1)=1/4, amit z=0, x=y=1/2 esetén, illetve a kezdetben z-re tett feltételt mellőzve szimmetria okok miatt még x=0, y=z=1/2, illetve y=1, x=z=1/2 esetén vesz fel.
1 feltétel mellett tehát legnagyobb értékét a c=1 helyen veszi fel. Ezek alapján S lehetséges legnagyobb értéke Smax =f(1)=1/4, amit z=0, x=y=1/2 esetén, illetve a kezdetben z-re tett feltételt mellőzve szimmetria okok miatt még x=0, y=z=1/2, illetve y=1, x=z=1/2 esetén vesz fel.
C értékét vizsgálva is feltehetjük, hogy z a legkisebb, ekkor 0 z
z 1/3. Mivel x,y
1/3. Mivel x,y z, innen y=1-z-x, ahol x tetszőleges eleme a [z,1-2z] intervallumnak. Rögzített z mellett vizsgáljuk az
z, innen y=1-z-x, ahol x tetszőleges eleme a [z,1-2z] intervallumnak. Rögzített z mellett vizsgáljuk az
f(x):=C=-x3+x2+(3z2-2z)x+(z3-2z2+z)
függvényt. Ennek deriváltja, f'(x)=-3x2+2x+(3z2-2z) pontosan akkor 0, ha x1=z, vagy x2=2/3-z. Mivel z 2/3-z és f főegyütthatója negatív, a [z,
2/3-z és f főegyütthatója negatív, a [z,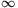 ) intervallumon f(x) maximumát az x=2/3-z helyen veszi fel. Mivel pedig 2/3-z
) intervallumon f(x) maximumát az x=2/3-z helyen veszi fel. Mivel pedig 2/3-z [z,1-2z], rögzített 0
[z,1-2z], rögzített 0 z
z 1/3 esetén C értéke akkor a lehető legnagyobb, ha x=2/3-z, y=1/3. Ekkor a
1/3 esetén C értéke akkor a lehető legnagyobb, ha x=2/3-z, y=1/3. Ekkor a
deriváltja g'(z)=-(3z-2)2/3, vagyis a g függvény szigorúan monoton csökken, a [0,1/3] intervallumban legnagyobb értékét a z=0 helyen veszi fel. Ezek alapján C lehetséges legnagyobb értéke Cmax =g(0)=4/27, amit z=0, y=1/3, x=2/3 esetén, illetve a kezdetben z-re tett feltételt mellőzve szimmetria okok miatt még x=0, z=1/3, y=2/3, illetve y=0, x=1/3, z=2/3 esetén vesz fel.
Statistics:
42 students sent a solution. 5 points: Almási 270 Gábor András, Blázsik Zoltán, Bodor Bertalan, Bogár 560 Péter, Csaba Ákos, Csizmadija Laura, Éles András, Grósz Dániel, Kunos Ádám, Nagy 314 Dániel, Sümegi Károly, Szalkai Balázs, Szalóki Dávid, Szűcs Gergely, Tóth 666 László Márton. 4 points: Cseh Ágnes, Fonyó Dávid, Honner Balázs, Lovas Lia Izabella, Mercz Béla, Peregi Tamás, Sárkány Lőrinc, Somogyi Ákos, Tossenberger Anna, Tóth 796 Balázs, Wolosz János, Zieger Milán. 3 points: 4 students. 2 points: 2 students. 0 point: 9 students.
Problems in Mathematics of KöMaL, January 2007
