Problem B. 3980. (February 2007)

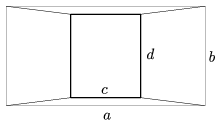
B. 3980. The Figure shows a polyhedron viewed from above. Its ``bases'' are parallel rectangles, its lateral edges are equal in length, and its height is m. Someone found the following formula for the volume of the polyhedron:

$V= \frac{m}{6} \big[(2a+c)b+ (2c+a)d\big].$

Is the formula correct?

(3 pont)

Deadline expired on March 19, 2007.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Vágjuk fel a poliédert 9 részre a fedőlap éleire illeszkedő függöleges síkok segítségével. A középső rész egy téglatest lesz, melynek térfogata mcd. A téglatest oldallapjaihoz illeszkedő 4 rész közül két-két szemköztit összetolva egy-egy háromszög alapú hasábot kapunk, melyek térfogata $\frac{1}{2}md(a-c)$ , illetve $\frac{1}{2}mc(b-d)$ . Végül a négy sarokrészt összeillesztve egy téglalap alapú gúla keletkezik, melynek térfogata $\frac{1}{3}m(a-c)(b-d)$ . Ezt a négy térfogatmennyiséget összeadva kis átalakítás után valóban a talált képletet kapjuk.

Statistics:

163 students sent a solution.

3 points: 97 students.

2 points: 20 students.

1 point: 32 students.

0 point: 14 students.

Problems in Mathematics of KöMaL, February 2007

163 students sent a solution.
3 points:	97 students.
2 points:	20 students.
1 point:	32 students.
0 point:	14 students.

Already signed up?
New to KöMaL?