 Problem B. 4009. (May 2007)
Problem B. 4009. (May 2007)
B. 4009. The angle bisectors drawn from the vertices A and B of a triangle ABC intersect the opposite sides at A1 and B1, respectively. P is the intersection of the ray A1B1 with the circumscribed circle of the triangle. Prove that
(5 pont)
Deadline expired on June 15, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Írjuk át a bizonyítandó állítást PB.PC=PA.PC+PA.PB alakba. A szokásos jelölések mellett jelölje R a körülírt kör sugarát, tXYZ az XYZ háromszög területét. Legyen továbbá t=tABC és q=PB1/A1B1, ekkor PA1/A1B1=1+q. A szögfelező-tételt felhasználva
ezért
Hasonlóképpen kapjuk, hogy
A PAB háromszög területének meghatározásához jelölje az X pontnak az AB egyenestől vett távolságást mX, és legyen m=mC. Ekkor
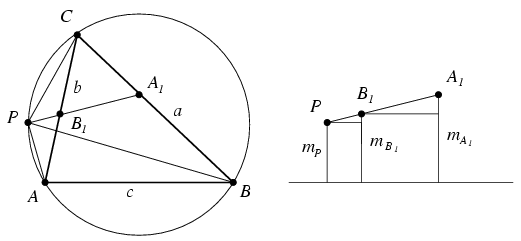
Ezért az ábráról leolvasható hasonlóságok alapján (az ábra az a>b esetet szemlélteti) mB1-mP=q(mA1-mB1), ahonnan
Következésképpen
tehát
Statistics:
8 students sent a solution. 5 points: Bogár 560 Péter, Dinh Van Anh, Fonyó Dávid, Honner Balázs, Tossenberger Anna, Wolosz János. 4 points: Cseh Ágnes, Réti Dávid.
Problems in Mathematics of KöMaL, May 2007
