Problem B. 4015. (September 2007)

B. 4015. The diagonals of a convex quadrilateral enclose an angle of 45^o. Drop a perpendicular from each vertex of the quadrilateral onto the line of the diagonal connecting the two adjacent vertices. Find the ratio of the area of the quadrilateral formed by the feet of the perpendiculars to the area of the original quadrilateral.

(Suggested by J. Bodnár, Budapest)

(3 pont)

Deadline expired on October 15, 2007.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Legyen az átlók metszéspontja O, a négyszög csúcsai valamilyen körüljárás szerint A,B,C,D. A jelölést válasszuk úgy, hogy az AOB szög 45^o-os legyen. A merőlegesek talppontjait jelölje értelemszerűen A',B',C',D'. Ezek a pontok rendre az OB,OA,OD,OC félegyeneseken helyezkednek el úgy, hogy minden esetben .

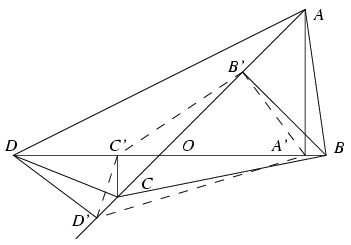
Mindkét négyszöget az átlói négy kis háromszögre bontanak fel, melyek páronként hasonlók egymáshoz. Nevezetesen, ha X és Y nem átellenes csúcsok, akkor az X'OY' háromszög hasonló az XOY háromszöghöz, a hasonlóság aránya , tehát az előbbi háromszög területe fele az utóbbiénak. Mindezek alapján az A'B'C'D' négyszög területe is feleakkora, mint az ABCD négyszögé.

Statistics:

160 students sent a solution.
3 points:	98 students.
2 points:	28 students.
1 point:	23 students.
0 point:	11 students.

Problems in Mathematics of KöMaL, September 2007