 Problem B. 4020. (September 2007)
Problem B. 4020. (September 2007)
B. 4020. Find two non-congruent polyhedra that both have the front elevation and plan shown below in the figure. (The common point in the inside is the centre of the square. The line segments of the squares are all visible edges, but there are no other invisible edges either.)
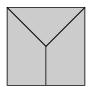
(5 pont)
Deadline expired on October 15, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Betűzzük meg az (E) elölnézeti és az (F) fölülnézeti rajzon látható csúcspontokat az ábrán látható módon. A keresett P poliéder egy ABCDEFGH kockában helyezkedik el, melynek elöl-, illetve felülnézete éppen a megfelelő rajzon látható négyzet. A kocka középpontját jelölje O.
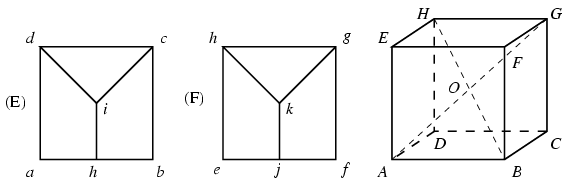
P-nek kell legyen egy olyan éle, mely elölnézetben a cd szakasz, nevezetesen annak az L lapnak az egyik éle, mely az (E) ábrán egy háromszögként jelenik meg. Ez tehát a kocka fedőlapján az EH és FG szakaszokat köti össze. Mivel ennek az élnek az (F) ábrán is jelentkeznie kell, ez csak az EF vagy a HG él lehet. Tegyük fel, hogy ez az EF él. Mivel jk felülről látható, de (E)-n csak egy pontként látszódhat, P-nek kell legyen egy éle, amely az EF szakasz felezőpontját az EFGH négyzet középpontjával köti össze, ám ekkor az erre illeszkedő lapok mind a fedőlap síkjába kell, hogy essenek, ami nem lehetséges. Tehát az L lap egyik éle HG, és ezért L mindkét nézeten háromszögként mutatkozik, tehát nem lehet más, mint a HGO háromszög.
A HO élhez csatlakozó másik lapra három lehetőség kínálkozik. Ha elölnézetben ahid, felülnézetben pedig ejkh lenne akkor a HAXO négyszögről lenne szó, ahol X az AB szakasz felezőpontja. Ekkor azonban ugyanabban a síkban lenne, mint az L lap, ami nem lehetséges. Ha elölnézete ahid, felülnézete pedig a hk szakasz, akkor a HDYO négyszögről van szó, ahol Y az ABCD négyzet középpontja. Ha pedig az (E) ábrán id, (F)-en pedig ejkh látszik belőle, akkor a HEZO négyszögről van szó, ahol Z az ABFE négyzet középpontja. Hasonló a helyzet a GO élhez csatlakozó lappal is.
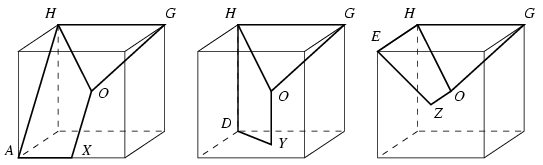
Anélkül, hogy minden lehetséges eset megvizsgálására törekednénk, tegyük fel, hogy a két szóban forgó lap HEZO és GFZO. Az EZ élhez az EDYZ vagy az EAXZ lap csatlakozhat még, az FZ élhez pedig az FCYZ vagy az FBXZ lap. Mivel EAXZ és FBXZ egy síkban vannak, szimmetria okok miatt két lényegesen különböző esetet vizsgálhatunk. Az első esetben a két szóban forgó lap EDYZ és FCYZ, a másodikban EDYZ és FBXZ. A E,D,Y,Z pontok azért vannak egy síkon, mert az YZ szakasz a DE szakaszból B középpontú, 1/2 arányú nagyítással kapható meg.
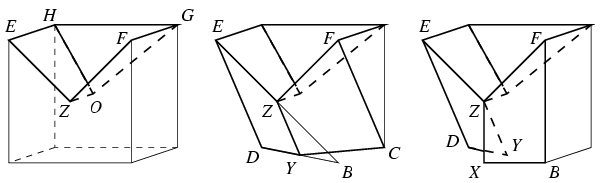
Miután a keresett poliéder 5 lapját ily módon megtaláltuk, P konstrukcióját mindkét esetben könnyen befejezhetjük. Az első esetben P további lapjai az YCD háromszög, a CDHG négyzet, valamint a DHE és CGF háromszögek lesznek. A második esetben 5 további lap van, ezek a DHE és XYZ háromszögek, a BCGF és CDHG négyzetek, valamint a BCDYX konkáv ötszög.
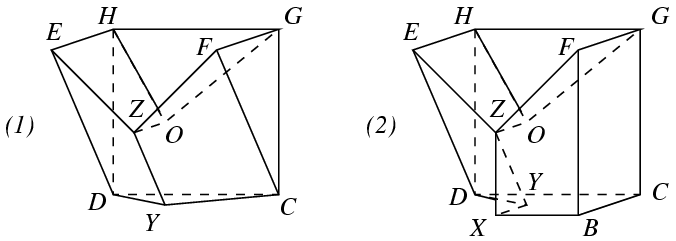
Mivel az első poliédernek 9, a másodiknak 10 lapja van, ezek nem egybevágók.
Statistics:
72 students sent a solution. 5 points: Bálint Dániel, Bodor Bertalan, Dinh Van Anh, Éles András, Fonyó Dávid, Horváth 385 Vanda, Huszár Kristóf, Kalina Kende, Keresztfalvi Tibor, Lakatos 707 Tamás, Lőrincz Dóra, Major Bálint István, Márkus Bence, Nagy 111 Miklós, Nagy 648 Donát, Nagy 729 Krisztina, Nagy-Baló András, Salát Zsófia, Somogyi Ákos, Tossenberger Anna, Tóth 369 László Márton, Varga 171 László. 3 points: 1 student. 2 points: 6 students. 0 point: 42 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, September 2007
