Problem B. 4023. (October 2007)

B. 4023. Construct two lines through a given point of one side of a triangle that divide the area of the triangle into three equal parts.

(3 pont)

Deadline expired on November 15, 2007.

Sorry, the solution is available only in Hungarian. Google translation

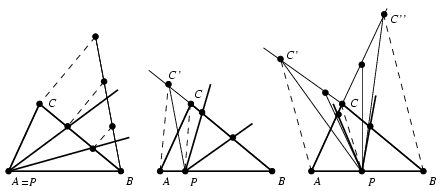
Megoldás: Ha az adott P pont az egyik csúcsba esik, akkor azt a szemközti oldal harmadolópontjaival kell összekötni, melyeket a párhuzamos szelők tételére támaszkodó ismert szerkesztési eljárással kapunk meg. Tegyük fel most, hogy P az ABC háromszög AB oldalának A-hoz közelebbi belső pontja. Ha ez épp az AB oldal H harmadolópontja, akkor nyilván C-vel, illetve a BC odal felezőpontjával kell azt összekötnünk.

Ha P az AH szakasz belső pontja, akkor húzzuk meg azt az egyenest, amely párhuzamos PC-vel és áthalad A-n. Ennek az egyenesnek a BC egyenessel alkotott metszéspontja legyen C'. Az ABC háromszög területe ugyanakkora, mint a PBC' háromszögé. Az előző módszerrel ez utóbbit a P csúcsán áthaladó két egyenessel harmadolhatjuk. Mivel C'B:CB=AB:PB>2/3, a C'B oldal minkét harmadolópontja a BC szakaszra esik, tehát az eredeti feladat megoldását is megkaptuk egyben.

Végül, ha P nem esik az AH szakaszra, akkor az előző módszerrel csak az egyik egyenest kapjuk meg, hiszen a BC' szakasznak csak a B-hez közelebbi harmadolópontja esik a BC oldalra. A másik egyenest most nyilván úgy kapjuk, hogy a PC-vel B-n át húzott párhuzamos AC-vel alkotott metszéspontját A-val összekötő szakasz A-hoz közelebbi harmadolópontját kötjük össze P-vel.

Statistics:

172 students sent a solution.
3 points:	82 students.
2 points:	64 students.
1 point:	5 students.
0 point:	19 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, October 2007