 Problem B. 4025. (October 2007)
Problem B. 4025. (October 2007)
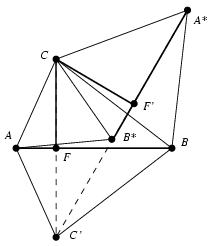
B. 4025. A regular triangle is drawn on the side BC of a triangle ABC towards the outside, and one on the side CA towards the inside. The third vertices of the regular triangles are A* and B*, respectively. The reflection of vertex C in the line AB is C'. Prove that the points A*, B* és C' are collinear.
(4 pont)
Deadline expired on November 15, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: A B*A* egyenest C körüli 60o-os elforgatással kapjuk az AB egyenesből. Ugyanez az elforgatás a CC' szakasz AB egyenesre eső F felezőpontját a B*A* egy F' pontjába viszi. Mivel CF merőleges AB-re, a B*A* egyenes merőleges CF'-re. Ezért elegendő belátni, hogy C'F' is merőleges CF'-re, ami viszont rögtön látszik abból, hogy a CC'F' háromszögben a CC' oldal kétszer olyan hosszú, mint a CF' oldal, közbezárt szögük pedig 60o.
Statistics:
136 students sent a solution. 4 points: 53 students. 3 points: 65 students. 2 points: 3 students. 1 point: 5 students. 0 point: 7 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, October 2007
