Problem B. 4026. (October 2007)

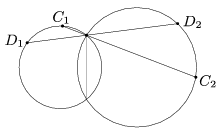
B. 4026. The length of the common chord of two circles of diameters d₁ and d₂ is h. A line drawn through one of the intersections cuts the circles at the points C₁ and C₂, and the points D₁ and D₂, respectively, as shown in the Figure. Prove that the line C₁D₁ is only perpendicular to C₂D₂ if $\frac{1}{h^2} = \frac{1}{d_1^2} + \frac{1}{d_2^2}$ .

(4 pont)

Deadline expired on November 15, 2007.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Az egyenesek metszéspontját jelölje A, a két kör másik metszéspontját B. A két egyenes hajlásszöge legyen $\alpha$ , ekkor a kerületi szögek tétele miatt

D₁BC₁ $\angle$ =D₁AC₁ $\angle$ = $\alpha$ =D₂AC₂ $\angle$ =D₂BC₂ $\angle$ .

Ugyancsak a kerületi szögek tétele miatt

$D_2C_2A\angle=D_2BA\angle=\beta\qquad\hbox{\rm \'es}\qquad C_1D_1A\angle=C_1BA\angle=\gamma.$

A B pontból a C₁C₂ és a D₁D₂ szakasz is ugyanakkora szög alatt látszik, ez a szög, melynek nagysága $\alpha$ + $\beta$ + $\gamma$ tehát független a két egyenes helyzetétől. Az MD₂D₁ szög nagysága $\alpha$ + $\beta$ , tehát a D₁D₂M háromszögből számolva a D₁MD₂ szög nagyságára 180^o-( $\alpha$ + $\beta$ + $\gamma$ ) adódik. Ez tehát pontosan akkor derékszög, ha a B pontból a D₁D₂ szakasz derékszög alatt látszik.

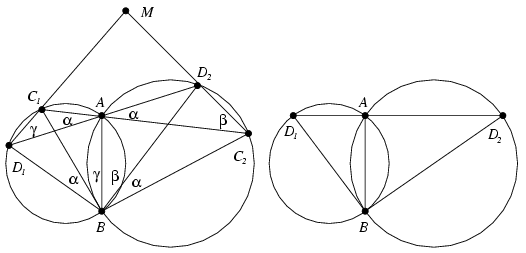
A fentiek miatt a két feltétel ekvivalenciájának vizsgálatánál feltehetjük, hogy a D₁D₂ szakasz merőleges AB-re, ekkor AB=h, D₁B=d₁ és D₂B=d₂. Az ezekre vonatkozó feltételt tehát így alakíthatjuk át:

$\frac{h^2}{d_1^2}+\frac{h^2}{d_2^2}=1\ \Leftrightarrow \frac{AB^2}{D_1B^2}=1-\frac{AB^2}{D_2B^2}=\frac{D_2B^2-AB^2}{D_2B^2}= \frac{AD_2^2}{BD_2^2}\ \Leftrightarrow \frac{AB}{D_1B}=\frac{AD_2}{BD_2}.$

Ez pontosan azt jelenti, hogy a D₁AB és BAD₂ derékszögű háromszögek hasonlók, vagyis hogy az ABD₂ szög az ABD₁ szöget 90^o-ra egészíti ki, ami, mint láttuk, ekvivalens azzal, hogy a C₁D₁ egyenes merőleges a C₂D₂ egyenesre.

Statistics:

47 students sent a solution.

4 points: Balla Attila, Blázsik Zoltán, Bodor Bertalan, Bohus Kinga, Botos Csongor, Dinh Hoangthanh Attila, Dinh Van Anh, Éles András, Fonyó Dávid, Grósz Dániel, Gyurcsik Judit, Hursán Zsófia, Marák Károly, Mészáros András, Nagy 648 Donát, Nagy-Baló András, Pasztuhov Anna, Peregi Tamás, Perjési Gábor, Rácz Tamás, Strenner Péter, Szabó 895 Dávid, Szalkai Balázs, Tossenberger Anna, Varga 171 László, Véges Márton.

3 points: Bartha Zsolt, Csányi János Dániel, Farkas Márton, Kalina Kende, Kiss 243 Réka, Kiss 902 Melinda Flóra, Márkus Bence, Pap Bálint, Piller Éva, Somogyi Ákos, Szórádi Márk, Szőke Nóra, Törcsvári Gergő.

2 points: 6 students.

0 point: 2 students.

Problems in Mathematics of KöMaL, October 2007

47 students sent a solution.
4 points:	Balla Attila, Blázsik Zoltán, Bodor Bertalan, Bohus Kinga, Botos Csongor, Dinh Hoangthanh Attila, Dinh Van Anh, Éles András, Fonyó Dávid, Grósz Dániel, Gyurcsik Judit, Hursán Zsófia, Marák Károly, Mészáros András, Nagy 648 Donát, Nagy-Baló András, Pasztuhov Anna, Peregi Tamás, Perjési Gábor, Rácz Tamás, Strenner Péter, Szabó 895 Dávid, Szalkai Balázs, Tossenberger Anna, Varga 171 László, Véges Márton.
3 points:	Bartha Zsolt, Csányi János Dániel, Farkas Márton, Kalina Kende, Kiss 243 Réka, Kiss 902 Melinda Flóra, Márkus Bence, Pap Bálint, Piller Éva, Somogyi Ákos, Szórádi Márk, Szőke Nóra, Törcsvári Gergő.
2 points:	6 students.
0 point:	2 students.

Already signed up?
New to KöMaL?