 Problem B. 4036. (November 2007)
Problem B. 4036. (November 2007)
B. 4036. The circles k1 and k2 touch each other on the outside at P. One of their common tangents not passing through P is e, which touches k1 and k2 at A and B, respectively. The line f is parallel to e, touches k1 at C and intersects k2 at D and E. Prove that the common chord of the circumcircles of the triangles ABC and ADE contains P.
(5 pont)
Deadline expired on December 17, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Mivel az AC szakasz a k1 kör átmérője, Thalesz tétele értelmében az APC szög derékszög. Ha a két kör P-n áthaladó közös érintője az e egyenest P'-ben metszi, akkor P'A=P'P=P'B, vagyis az APB szög is 90o-os, P tehát illeszkedik a BC szakaszra. Mivel a CAB szög is 90o-os, ez a szakasz az ABC háromszög köré írt k3 kör egyik átmérője, amely merőleges AP-re. Ha tehát az A pontot P-re tükrözzük, akkor az így kapott A' pont a k3 körön helyezkedik el. Erre a pontra BA=BA'. Ha megmutatjuk, hogy az ADE háromszög köré írható k4 kör középpontja éppen B, akkor ebből következik, hogy A' is a k4 körön van, vagyis éppen AA' lesz a k3 és k4 körök közös húrja. Mivel ez illeszkedik P-re, a feladat állítása ebből már következik.
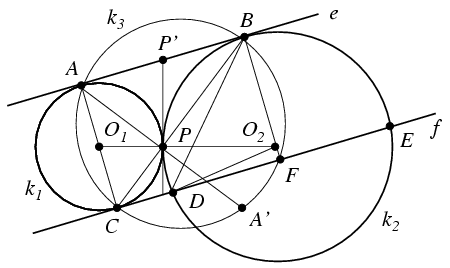
Mivel BD=BE, elegendő annyit megmutatni, hogy BA=BD. Legyen a körök középpontja O1,O2, sugara r1,r2, a DE szakasz felezőpontja pedig F. Az O1ABO2 derékszögű trapézból kiindulva, a Pithagorasz tétel alapján AB2+(BO2-AO1)2=O1O22, vagyis
AB2=(r1+r2)2-(r2-r1)2=4r1r2.
A DFO2 esetleg elfajuló derékszögű háromszögből r22=DF2+(2r1-r2)2, tehát a DFB derékszögű háromszögre is felírva a Pithagorasz tételt
BD2=DF2+FB2=r22-(2r1-r2)2+(2r1)2=4r1r2=BA2,
ahonnan valóban BD=BA következik.
Statistics:
40 students sent a solution. 5 points: Bodor Bertalan, Dinh Hoangthanh Attila, Dinh Van Anh, Éles András, Fonyó Dávid, Gévay Gábor, Gyurcsik Judit, Horváth 385 Vanda, Hursán Zsófia, Kalina Kende, Kiss 243 Réka, Márkus Bence, Nagy 648 Donát, Piller Éva, Somogyi Ákos, Strenner Péter, Szabó 313 Gábor, Szabó 895 Dávid, Szalai Zsófia, Szalkai Balázs, Szőke Nóra, Tossenberger Anna, Tóth 369 László Márton, Varga 171 László, Weisz Ágoston, Zieger Milán. 4 points: Bencs 111 Ferenc, Blázsik Zoltán, Bohus Kinga, Keresztfalvi Tibor, Lovas Lia Izabella, Marák Károly. 3 points: 2 students. 2 points: 3 students. 0 point: 2 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, November 2007
