Problem B. 4045. (December 2007)

B. 4045. An equilateral triangle of unit side is moved between the arms of a 120^o angle XOY so that vertex A lies on the arm OX, vertex B lies on the arm OY, and the line AB separates the points C and O. Determine the locus of vertex C.

(4 pont)

Deadline expired on January 15, 2008.

Sorry, the solution is available only in Hungarian. Google translation

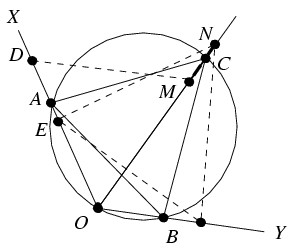
Megoldás: Az OX szögszáron jelölje D és E azt a pontot, amely O-tól 1, illetve $1/\sqrt{3}$ távolságra van. Ha A=D, akkor C az XOY szög felezőjének az az M pontja, amely O-tól 1 távolságra van, ha pedig A=E, akkor C a szögfelezőnek azon N pontja lesz, amely O-tól $2/\sqrt{3}$ távolságra van. Belátjuk, hogy a keresett mértani hely éppen az MN szakasz.

Mivel az AOBC négyszög húrnégyszög, az AOC szög is 60^o-os, tehát C a szögfelezőre esik. Az OA=x, OB=y jelöléssel az AOBC húrnégyszögre a Ptolemaiosz tételt felírva kapjuk, hogy OC=x+y. Az AOB háromszögre a koszinusz tételt felírva x²+y²+xy=1, ahonnan OC²=(x+y)²=1+xy. Mivel a fenti összefüggés miatt (x-y)²=1-3xy is igaz,

$1\le 1+xy=OC^2=\frac{4}{3}-\frac{1}{3}(x-y)^2\le \frac{4}{3},$

ahonnan $1\le OC\le 2/\sqrt{3}$ , vagyis C valóban az MN szakaszon helyezkedik el. Ha a háromszöget folytonosan úgy mozgatjuk, hogy az A csúcs D-ből E-be kerüljön, akkor a C csúcs is folytonosan vándorol át az M pontból N-be, vagyis az egész MN szakaszt befutja.

Statistics:

86 students sent a solution.

4 points: Aujeszky Tamás, Bartha Zsolt, Blázsik Zoltán, Bodor Bertalan, Dinh Hoangthanh Attila, Dinh Van Anh, Dudás 002 Zsolt, Éles András, Farkas Márton, Fonyó Dávid, Frankl Nóra, Huszár Kristóf, Kiss 243 Réka, Konkoly 001 Csaba, Kovács 999 Noémi, Kristóf Panna, Lovas Lia Izabella, Marák Károly, Márkus Bence, Mészáros András, Peregi Tamás, Salát Zsófia, Szabó 895 Dávid, Szőke Nóra, Tossenberger Anna, Tóth 369 László Márton, Tubak Dániel, Varga 171 László, Véges Márton.

3 points: Aczél Gergely, Anda Roland, Bohus Kinga, Gőgös Balázs, Grósz Dániel, Horváth 385 Vanda, Keresztfalvi Tibor, Mihálykó Ágnes, Nagy-Baló András, Palincza Richárd, Pasztuhov Anna, Perjési Gábor, Piller Éva, Prok Tamás, Somogyi Ákos, Szalkai Balázs, Tóth Bence Barnabás.

2 points: 16 students.

1 point: 17 students.

0 point: 6 students.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, December 2007

86 students sent a solution.
4 points:	Aujeszky Tamás, Bartha Zsolt, Blázsik Zoltán, Bodor Bertalan, Dinh Hoangthanh Attila, Dinh Van Anh, Dudás 002 Zsolt, Éles András, Farkas Márton, Fonyó Dávid, Frankl Nóra, Huszár Kristóf, Kiss 243 Réka, Konkoly 001 Csaba, Kovács 999 Noémi, Kristóf Panna, Lovas Lia Izabella, Marák Károly, Márkus Bence, Mészáros András, Peregi Tamás, Salát Zsófia, Szabó 895 Dávid, Szőke Nóra, Tossenberger Anna, Tóth 369 László Márton, Tubak Dániel, Varga 171 László, Véges Márton.
3 points:	Aczél Gergely, Anda Roland, Bohus Kinga, Gőgös Balázs, Grósz Dániel, Horváth 385 Vanda, Keresztfalvi Tibor, Mihálykó Ágnes, Nagy-Baló András, Palincza Richárd, Pasztuhov Anna, Perjési Gábor, Piller Éva, Prok Tamás, Somogyi Ákos, Szalkai Balázs, Tóth Bence Barnabás.
2 points:	16 students.
1 point:	17 students.
0 point:	6 students.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?