 Problem B. 4059. (January 2008)
Problem B. 4059. (January 2008)
B. 4059. O is a given point in the plane. Give an example for congruent triangles A and B, such that every circle centred at O has parts of the equal areas inside the triangles A and B.
Inspired by a problem of the Schweitzer Competition of 2007
(5 pont)
Deadline expired on February 15, 2008.
Sorry, the solution is available only in Hungarian. Google translation
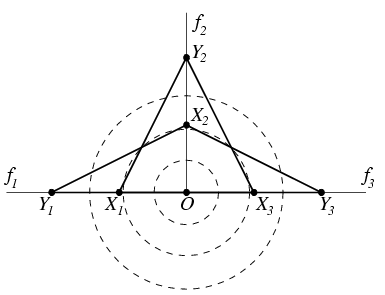
Megoldás: Vegyük fel úgy az O-ból induló f1, f2, f3 félegyeneseket, hogy f1 és f3 ne essenek egybe, de mindkettő derékszöget zárjon be az f2 félegyenessel. Az fi félegyenesen jelöljük ki az Xi,Yi pontokat úgy hogy OX1=OX2=OX3<OY1=OY2=OY3 legyen. Mivel OX1Y2, OX2Y1, OX3Y2 és OX2Y3 egymással egybevágó derékszögű háromszögek, minden O középpontú körvonalnak ugyanolyan hosszúságú része esik ezek mindegyikébe. Innen azonnal látszik, hogy az egymással nem egybevágó A=Y1X2Y3 és B=X1Y2X3 háromszögek megfelelők lesznek.
Statistics:
27 students sent a solution. 5 points: Aczél Gergely, Bálint Dániel, Blázsik Zoltán, Bodor Bertalan, Dinh Hoangthanh Attila, Énekes Péter, Kalina Kende, Keresztfalvi Tibor, Kiss 716 Eszter, Kovács 999 Noémi, Márkus Bence, Mezei Márk, Misnyovszki Péter, Perjési Gábor, Tóth 369 László Márton, Tóth Bence Barnabás, Tubak Dániel, Varga 171 László, Wang Daqian, Zieger Milán. 4 points: Gele Viktória, Huszár Kristóf, Nagy 729 Krisztina, Vajk Dóra. 0 point: 3 students.
Problems in Mathematics of KöMaL, January 2008
