 Problem B. 4067. (February 2008)
Problem B. 4067. (February 2008)
B. 4067. Erect a perpendicular to each of the sides AB, BC, CA of a triangle of perimeter k at the vertices A, B, C, respectively. Let K denote the perimeter of the new triangle obtained from the perpendiculars. Prove that , where
 ,
,  and
and  are the angles of the triangle ABC.
are the angles of the triangle ABC.
(3 pont)
Deadline expired on March 17, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Az új háromszög csúcsait jelölje az ábrán látható módon A',B',C'. Mivel a szerkesztés során merőleges szárú szögek lépnek fel, az A'B'C' háromszög hasonló az eredeti ABC háromszöghöz. Ábránk ezt a hegyesszögű esetben szemlélteti, de könnyen ellenőrizhető, hogy ez mindig így lesz. Azt kell tehát csak megmutatnunk, hogy a hasonlóság aránya ctg +ctg
+ctg +ctg
+ctg .
.
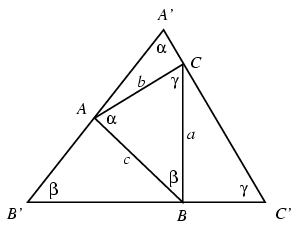
Feltehetjük, hogy  ,
, <90o, ekkor a B csúcs az ábrán látható módon elválasztja a B' és C' pontokat, vagyis
<90o, ekkor a B csúcs az ábrán látható módon elválasztja a B' és C' pontokat, vagyis
Azt szeretnénk megmutatni, hogy B'C'=a(ctg +ctg
+ctg +ctg
+ctg ). A fenti összefüggés és a szinusz-tétel alapján ez azzal ekvivalens, hogy
). A fenti összefüggés és a szinusz-tétel alapján ez azzal ekvivalens, hogy
Ha sin  -val felszorzunk, akkor az ezzel egyenértékű
-val felszorzunk, akkor az ezzel egyenértékű
sin  =sin
=sin  cos
cos  +sin
+sin  cos
cos 
összefüggésre jutunk, ami pedig nyilván teljesül, hiszen sin  =sin (180o-
=sin (180o- -
- )=sin (
)=sin ( +
+ ).
).
Statistics:
52 students sent a solution. 3 points: Aczél Gergely, Ágoston Tamás, Anda Roland, Balázs Barbara Anna, Balla Attila, Bencs 111 Ferenc, Blázsik Zoltán, Bodor Bertalan, Csere Kálmán, Deák Zsolt, Eckert János, Farkas Márton, Fonyó Dávid, Földi Sándor, Fukker Gábor, Gyurcsik Judit, Héricz Dalma, Hursán Zsófia, Huszár Kristóf, Kiss 902 Melinda Flóra, Kovács 235 Gábor, Lenger Dániel, Lovas Lia Izabella, Marák Károly, Mészáros András, Mihálykó Ágnes, Müller Márk, Nagy Róbert, Nguyen Sy Bang, Paripás Viktor, Peregi Tamás, Petróczy Dóra Gréta, Réti Dávid, Salát Zsófia, Szabó 895 Dávid, Szalai Szilárd, Szalkai Balázs, Szegedy Lóránt, Szepesvári Dávid, Szórádi Márk, Ta Phuong Linh, Vajk Dóra, Varju 105 Tamás, Wagner Zsolt, Weisz Ágoston, Welsz Edit, Zieger Milán, Zsupanek Alexandra. 2 points: Bartha Éva Lili. 1 point: 3 students.
Problems in Mathematics of KöMaL, February 2008
