Problem B. 4070. (February 2008)

B. 4070. The positive integers a and b, written in decimal system, can be obtained from each other by rearranging their digits. Prove that

a) the sum of the digits of 2a equals that of 2b;

b) if both a and b are even, then the sum of the digits of $\frac{a}{2}$ equals that of $\frac{b}{2}$ .

Kvant

(5 pont)

Deadline expired on March 17, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Ha n,m természetes számok, akkor jelölje S(n) az n számjegyeinek összegét, és legyen n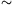 $\sim$ m, ha n és m megkaphatók egymásból számjegyeik sorrendjének megváltoztatásával. Az első állítás azt jelenti, hogy ha a 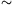$\sim$ b, akkor S(2a)=S(2b). Minthogy pedig nyilván S(10n)=S(n), a második állításhoz elegendő azt megmutatnunk, hogy ha a 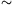$\sim$ b, akkor S(5a)=S(5b). Tegyük fel, hogy az n szám számjegyei sorban $n_k,n_{k-1},\ldots,n_0$ . Az alábbiakban megvizsgáljuk, mik lesznek a 2n, illetve az 5n számok számjegyei.

Ha i $\in$ {2,5} és j tetszőleges számjegy, akkor legyen f_i(j) az ij szám utolsó számjegye, g_i(j) pedig az ij szám első számjegye, amennyiben ij kétjegyű, különben pedig legyen 0. Világos, hogy f₂(j) $\in$ {0,2,4,6,8}, g₂(j) $\in$ {0,1}, f₅(j) $\in$ {0,5} és g₅(j) $\in$ {0,1,2,3,4}, vagyis tetszőleges j számjegyre és i $\in$ {2,5} indexre teljesül, hogy 0 $\le$ f_i(j)+g_i(j) $\le$ 9. Ha még az n_k+1=n_-1=0 jelölést is bevezetjük, akkor in utolsó számjegye f_i(n₀)=f_i(n₀)+g_i(n_-1) lesz, és $\alpha$ szerinti teljes indukcióval kapjuk, hogy a legfeljebb k+2 jegyű in számban a $10^\alpha$ helyiértéken álló számjegy éppen $f_i(n_\alpha)+g_i(n_{\alpha-1})$ lesz tetszőleges 0 $\le$ $\alpha$ $\le$ k+1 esetén (ha történetesen g_i(n_k)=0, akkor in-nek csak k+1 számjegye lesz). Innen rögtön leolvasható, hogy i $\in$ {2,5} esetén

$S(in)=\sum_{\alpha=0}^{k+1}f_i(n_\alpha)+\sum_{\alpha=-1}^{k}g_i(n_\alpha) =\sum_{\alpha=0}^{k}(f_i(n_\alpha)+g_i(n_\alpha)),$

ami csak az n számjegyeitől függ, de független azok sorrendjétől. Ez pedig egyszerre igazolja mindkét állítást.

Statistics:

85 students sent a solution.

5 points: 60 students.

4 points: 18 students.

3 points: 2 students.

2 points: 1 student.

1 point: 2 students.

0 point: 2 students.

Problems in Mathematics of KöMaL, February 2008

85 students sent a solution.
5 points:	60 students.
4 points:	18 students.
3 points:	2 students.
2 points:	1 student.
1 point:	2 students.
0 point:	2 students.

Already signed up?
New to KöMaL?