Problem B. 4083. (April 2008)

B. 4083. Each of the digits 0 to 9 is written in 10 fields of a 10×10 table. Is it possible that every row and every column has at most 4 different digits in it?

Kvant

(4 pont)

Deadline expired on May 15, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Először megmutatjuk, hogy egy 5×5-ös táblázat mezőibe be lehet írni a 0,1,2,3,4 számjegyeket úgy, hogy mindegyik pontosan 5-ször szerepel, továbbá minden oszlopban pontosan 2, minden sorban pedig pontosan 3 különböző számjegy fordul elő. Egy lehetséges ilyen elrendezés a következő:

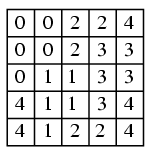
Két ilyen táblázatot egymás mellé helyezve egy 5×10-es táblázat kitöltését kapjuk a 0,1,2,3,4 számjegyekkel úgy, hogy mindegyik pontosan 10-szer szerepel, és továbbra is minden oszlopban pontosan 2, minden sorban pedig pontosan 3 különböző számjegy fordul elő. Egy 10×10-es táblázat megfelelő kitöltését kaphatjuk ebből úgy, hogy egy ilyen módon kitöltött 5×10-es táblázat alá helyezünk egy másikat oly módon, hogy abban minden egyes számjegyet a nála 5-tel nagyobbal helyettesítünk. (Ezzel még azt is elértük, hogy a sorokban csak 3 különböző számjegy szerepeljen.)

Statistics:

90 students sent a solution.
4 points:	82 students.
2 points:	1 student.
0 point:	3 students.
Unfair, not evaluated:	4 solutionss.

Problems in Mathematics of KöMaL, April 2008