Problem B. 4105. (September 2008)

B. 4105. Point A moves along one arm of an angle of vertex C and point B moves along the other arm so that CA+CB=1 remains valid. Prove that there exists a point that lies on the perpendicular bisectors of AB in all positions.

(4 pont)

Deadline expired on October 15, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Az A, illetve B pont C-től legtávolabb eső helyzetét a megfelelő szögszáron jelölje A₀ és B₀, ekkor CA₀=CB₀=1. Az A₀CB₀ háromszög köré írható kör középpontját jelölje O, ez éppen a CA₀ és CB₀ szakaszok felező merőlegeseinek metszéspontja. Ha létezik az állításnak megfelelő pont, az nem lehet más, mint az O pont.

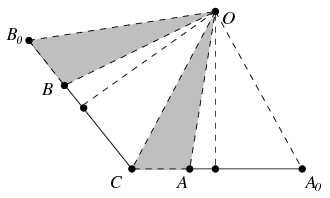
Mivel A₀OC és COB₀ egybevágó egyenlőszárú háromszögek, az előbbi egy O körüli forgatással átvihető az utóbbiba. Ez a forgatás tehát az A₀C szakaszt a CB₀ szakaszba viszi. Ha CA+CB=1, akkor B₀B=1-BC=CA, vagyis a forgatás az A pontot éppen B-be viszi, ezért OA=OB, vagyis O valóban rajta van az AB szakasz felező merőlegesén.

Statistics:

125 students sent a solution.
4 points:	86 students.
3 points:	13 students.
2 points:	11 students.
1 point:	3 students.
0 point:	12 students.

Problems in Mathematics of KöMaL, September 2008